Как сделать расчет угла наклона крыши

Деление рулеткой на несколько частей

Используя обыкновенную ленту рулетки можно легко разделить рабочую поверхность или заготовку на требуемое количество равных частей. Данный метод подходит в первую очередь для больших поверхностей – для труб или кабель каналов уже не сработает.

Как вы поступаете обычно? Замеряете общую длину или ширину, затем делаете вычисления и делите расстояние на нужное количество частей. После чего вновь линейкой или рулеткой отмеряете на поверхности эти части.

Оказывается все это можно проделать без калькулятора и даже без вычислений. Берете на рулетке число, которое больше чем ширина заготовки, и при этом кратно той величине, на которое вы хотите разделить расстояние.

Например ширина доски 17см, а вам ее нужно разделить на четыре равные части. Сдвигаете рулетку по диагонали до ближайшей отметки в 20см. После чего легко делите эти 20см на 4 и отмечаете метки на расстояниях 5см, 10см, 15см, 20см.

В итоге вы всего одним движением рулетки разделили поверхность на нужное количество частей.

Захотели поделить на 6 частей – ничего сложного. Можно сдвинуть диагональ до 30см и проделать то же самое.

Еще рулеткой на круглой трубе можно точно отмерить поперечный срез. Для этого плотно прижимаете по периметру трубы ленту, совместив концы. Если совместили ровно, никак иначе как под углом в 90 градусов она не ляжет.

Чем шире лента рулетки, тем предпочтительней. Проделать такой же фокус можно и с простым листком бумаги.

Когда невозможно измерить диаметр трубы или заготовки с торца, опять поможет строительная рулетка и геометрия. Обхватываете трубу лентой и измеряете ее окружность. После чего полученный результат нужно разделить на число Пи = 3,14. Это и будет необходимый диаметр.

Еще раз применив знания геометрии, строительной рулеткой без угольников и других инструментов можно проверить точность прямого угла. Как вы знаете из школьного курса – сумма квадратов катетов прямоугольного треугольника равна квадрату гипотенузы.

Берете любую поверхность где должен быть прямой угол, например две стены комнаты. Отмеряете рулеткой в одну сторону 30см, а в другую 40см и ставите метки. Если угол действительно прямой и строители не накосячили, то соединив эти две метки по гипотенузе, вы должны получить на рулетке расстояние ровно в 50см.

Такой метод применим к любым поверхностям и изделиям. Главное что вам нужно соблюдать при измерении – это пропорции 3 -4 -5.

Если вы еще не приобрели себе рулетку, подобрать необходимую модель и ознакомиться с текущими ценами на них можно здесь.

Онлайн калькулятор

Чтобы вычислить длины сторон прямоугольного треугольника вам нужно знать следующие параметры (либо-либо):

• для гипотенузы (с):
  • длины катетов a и b
  • длину катета (a или b) и прилежащий к нему острый угол (β или α, соответственно)
  • длину катета (a или b) и противолежащий к нему острый угол (α или β, соответственно)
• для катета:
  • длину гипотенузы (с) и длину одного из катетов
  • длину гипотенузы (с) и прилежащий к искомому катету (a или b) острый угол (β или α, соответственно)
  • длину гипотенузы (с) и противолежащий к искомому катету (a или b) острый угол (α или β, соответственно)
  • длину одного из катетов (a или b) и прилежащий к нему острый угол (β или α, соответственно)
  • длину одного из катетов (a или b) и противолежащий к нему острый угол (α или β, соответственно)

Введите их в соответствующие поля и получите результат.

Найти гипотенузу (c)

Найти гипотенузу по двум катетам

Катет a = Катет b = Гипотенуза c =

Чему равна гипотенуза (сторона с) если известны оба катета (стороны a и b)?

Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов:

c² = a² + b²

следовательно: c = √a² + b²

Пример

Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 3 см, а катет b = 4 см:

c = √3² + 4² = √9 + 16 = √25 = 5 см

Найти гипотенузу по катету и прилежащему к нему острому углу

Катет (a или b) = Прилежащий угол (β или α) = Гипотенуза c =

Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и прилежащий к нему угол?

c = a/_cos(β) = b/_cos(α)

Пример

Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а прилежащий к нему ∠β = 60°:

c = 2 / cos(60) = 2 / 0.5 = 4 см

Найти гипотенузу по катету и противолежащему к нему острому углу

Катет (a или b) = Противолежащий угол (α или β) = Гипотенуза c =

Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и противолежащий к нему угол?

c = a/_sin(α) = b/_sin(β)

Пример

Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а противолежащий к нему ∠α = 30°:

c = 2 / sin(30) = 2 / 0.5 = 4 см

Найти гипотенузу прямоугольного треугольника только по двум острым углам невозможно.

Найти катет

Найти катет по гипотенузе и катету

Гипотенуза c = Катет _{(известный)} = Катет _{(искомый)} =

Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и второй катет?

a = √c² — b²

b = √c² — a²

Пример

Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 5 см, а катет b = 4 см:

a = √5² — 4² = √25 — 16 = √9 = 3 см

Найти катет по гипотенузе и прилежащему к нему острому углу

Гипотенуза c = Угол (прилежащий катету) = °Катет =

Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и прилежащий к искомому катету острый угол?

a = c ⋅ cos(β)

b = c ⋅ cos(α)

Пример

Для примера посчитаем чему равен катет b прямоугольного треугольника если гипотенуза c = 5 см, а ∠α = 60°:

b = 5 ⋅ cos(60) = 5 ⋅ 0.5 = 2.5 см

Найти катет по гипотенузе и противолежащему к нему острому углу

Гипотенуза c = Угол (противолежащий катету) = °Катет =

Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и противолежащий к искомому катету острый угол?

a = c ⋅ sin(α)

b = c ⋅ sin(β)

Пример

Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 4 см, а ∠α = 30°:

a = 4 ⋅ sin(30) = 4 ⋅ 0.5 = 2 см

Найти катет по второму катету и прилежащему к нему острому углу

Катет (известный) = Угол (прилежащий известному катету) = °Катет (искомый) =

Чему равен один из катетов прямоугольного треугольника если известен другой катет и прилежащий к нему острый угол?

a = b ⋅ tg(α)

b = a ⋅ tg(β)

Пример

Для примера посчитаем чему равен катет b прямоугольного треугольника если катет a = 2 см, а ∠β = 45°:

b = 2 ⋅ tg(45) = 2 ⋅ 1 = 2 см

Найти катет по второму катету и противолежащему к нему острому углу

Катет (известный) = Угол (противолежащий известному катету) = °Катет (искомый) =

Чему равен один из катетов прямоугольного треугольника если известен другой катет и противолежащий к нему острый угол?

a = b / tg(β)

b = a / tg(α)

Пример

Для примера посчитаем чему равен катет a прямоугольного треугольника если катет b = 3 см, а ∠β = 35°:

a = 3 / tg(35) ≈ 3 / 0.7 ≈ 4.28 см

Примеры решений практических задач

1) решить треугольник по двум сторонам и противолежащему углу, т.е. углу между ними. Даны стороны а = 12 см, b = 8 см, угол=60°. Для того, чтобы решить задачу, требуется указать в онлайн-форме на данной странице условия задачи. В поле для стороны «a» указывается 12, в поле для стороны «b» ставится 8, в поле для углов «A» указывается 60. Нажать «Решить».

В ходе решения задачи получаем ответ: сторона c = 13,8 см; угол B = 35,2644° = 35°15’52» = 35°16′ = 0,1959π = 0,6155 rad; угол C = 84,7356° = 84°44’8» = 84°44′ = 0,4708π = 1,4789 rad; Периметр = 33,8 см; Полупериметр = 16,9 см; Площадь = 47,7984 см2; Высота h_a = 7,9664 см; Высота h_b = 11,9496 см; Высота h_c = 6,9273 см; Медиана m_a = 9,5513 см; Медиана m_b = 12,2958 см; Медиана m_c = 7,5107 см; Радиус окружности R, описанной около треугольника = 6,9291 см; Радиус окружности r, вписанной в треугольник = 2,8283 см. Таким образом, был найден угол треугольника по двум сторонам и углу.

2) как найти угол треугольника, зная его стороны или решите треугольник по трем сторонам. Даны три стороны a = 2 см, b = 3 см, c = 4 см. В поле онлайн-формы «a» ставим 2, в поле «b» указываем 3, в поле «c» ставим 4. Далее следует нажать «Решить».

Используя теорему косинусов, получаем угол A = 28,955° = 28°57’18» = 28°57′ = 0,1609π = 0,5054 rad; угол B = 46,5675° = 46°34’3» = 46°34′ = 0,2587π = 0,8128 rad; угол C = 104,4775° = 104°28’39» = 104°29′ = 0,5804π = 1,8235 rad; Периметр = 9 см; Полупериметр = 4,5 см; Площадь = 2,9046 см2; Высота h_a = 2,9046 см; Высота h_b = 1,9364 см; Высота h_c = 1,4523 см; Медиана m_a = 3,3912 см; Медиана m_b = 2,7839 см; Медиана m_c = 1,5811 см; Радиус окружности R, описанной около треугольника = 2,0657 см; Радиус окружности r, вписанной в треугольник = 0,6455 см.

Таким образом, были найдены все углы треугольника.

3) решить треугольник по двум углам и стороне. В треугольнике ABC сторона a = 5 см, два угла B = 30°, C = 45°. Ответ: сторона b = 2,59 см; сторона c = 3,66 см; угол A = 105° = 0,5833π = 1,8326 rad; Периметр = 11,25 см; Полупериметр = 5,625 см; Площадь = 4,5785 см2; Высота h_a = 1,8314 см; Высота h_b = 3,5355 см; Высота h_c = 2,5019 см; Медиана m_a = 1,9488 см; Медиана m_b = 4,1857 см; Медиана m_c = 3,537 см; Радиус окружности R, описанной около треугольника = 2,588 см; Радиус окружности r, вписанной в треугольник = 0,814 см.

Минимальный показатель уклона

Кровля считается главным материалом при устройстве верхней поверхности крыши, она также требует соблюдения определённых правил уклона в зависимости от её вида.

1. Если с профнастилом используется угол с показателем в 12 градусов, то для металлочерепицы такой показатель нужно увеличить до пятнадцати градусов.
2. Мягкая черепица может быть уложена на крышу с уклоном в одиннадцать градусов. В этом случае нужно учитывать особенности сплошной облицовки.
3. При укладке керамической черепицы показатель наклона должен доходить до 22 градусов.
4. Также нужно учитывать и то, что стропильная система подаётся большой нагрузке в случае ската с небольшой наклонностью. Чтобы избежать перегрузки ската во время строительства, нужно обязательно помнить о рекомендуемом наклоне.
5. Минимальный показатель уклона кровли из сэндвич-панелей доходит до пяти градусов, если в панелях конструкции в дальнейшем будут находиться окна, то такой показатель возрастает до семи градусов.

Самостоятельное определение уклона крыши

Чтобы изменить общий угол ската, можно применить специальный прибор, который поможет не тратить вам своё свободное время. Название такого инструмента — уклономер.

Также можно воспользоваться механическим угломером — более бюджетный вариант, но при этом не исключены длительная морока с таким устройством, особенно в том случае, если владелец использует инструмент первый раз.

Перед началом измерения необходимо понять общую специфику устройства:

1. Стандартный тип угломера без электронных функций выглядит как рейка с зафиксированной рамой. На стыке планок расположена ось, на который закреплён маятник. В его комплект входит пара колец, грузик, указатель, а также пластина. В дополнение к такому прибору идёт шкала с делениями, которая расположена на внутренней части выреза. Если расположить рейку по горизонтали, то указатель будет совпадать с нулевым делением шкалы.
2. Теперь следует рассмотреть главный процесс измерения, для которого и был создан данный прибор. Для начала рейку угломера следует выставить перпендикулярно по отношению к коньку. После на шкале маятника будет указана нужная величина в градусном показателе.
3. Способ, который основан на самостоятельном расчёте здания для изменения наклона с помощью проведения математический вычислений, не так эффективен. Чтобы измерить наклон крыши самостоятельно, для начала нужно определить длину катетов и гипотенузы. Если же говорить об измерении наклона кровли, то в этом случае прямая ската и станет гипотенузой.
4. После рассчитывается длина противолежащего и прилежащего катетов. Первым катетом является расстояние, которое разделяет конёк и перекрытие, а размер второго нужно принимать в виде расстояния между серединой перекрытия и карнизным свесом на одном из скате.
5. В этом случае после получения двух значений для нахождения третьего используется правило тригонометрии. В результате, зная синус, косинус либо тангенс (всё будет зависеть от размера составляющих), через инженерный калькулятор происходит вычисление цифрового показателя наклона крыши в процентном соотношении.

Если говорить о нагрузке, то лучше не выбирать минимальный показатель наклона, так как это может отрицательно повлиять на новую крышу. Если же кровля плоская, и изменить её не получится, то нужно обязательно использовать укрепительные редуты.

В общем расчёте цены не нужно забывать о массе общей конструкции дома и помнить о нагрузке от осадков — это поможет выявить не только правильный, но также и более экономичный метод для вас и вашего бюджета.

Если уклон ската доходит до 10 градусов, то лучше всего подойдёт отделка из гравия, до 20 градусов — шифер, а также профнастил. Стальные и медные листки лучше всего использовать в больших конструкциях, когда показатель верхнего румба варьируется от 50 до 60 градусов.

Величина нагрузок внешней среды

Ещё одним важным фактором в этом случае считается значение угла наклона кровли при воздействии на него внешних нагрузок, которые выпадают на конструкцию крыши.

В это случае можно заметить определённую связь. Можно заранее вычислить все линейные размеры и углы, но в итоге всё равно придётся провести деталировку. Нужно чётко определить, из какого материала будут создаваться узлы стропильной системы и детали, какова длина их сечения, шаг расположения, а также максимальная длина между двумя точками опоры, метод крепления элементов и их установка на несущие стены дома. Кроме собственного веса, на уклон большое влияние оказывает воздействие из внешней среды.

Калькулятор уклонов

Онлайн калькулятор

Посчитать уклон

Расстояние L = Превышение h =

Посчитать превышение

Уклон α = Расстояние L =

Посчитать расстояние

Уклон α = Превышение h =

Как посчитать уклон

Для того чтобы посчитать уклон вам, для начала, необходимо знать расстояние (L) и превышение (h). Далее следуйте формулам:

В процентах:

Уклон в % = h / L ⋅ 100

В промилле:

Уклон в ‰ = h / L ⋅ 1000

В градусах:

Уклон в ° = arctg ( h /_L)

Для примера рассчитаем уклон дороги в процентах: на дистанции в L = 500 м дорога поднимается на h = 30 м:

Уклон дороги = 30/500 ⋅ 100 = 6%

Как посчитать превышение

Чтобы вычислить превышение (h), надо знать расстояние (L) и уклон (в процентах, в промилле или в градусах).

Если уклон в процентах (%):

h = L ⋅ Уклон в % /₁₀₀

Если уклон в промилле (‰):

h = L ⋅ Уклон в ‰ /₁₀₀₀

Если уклон в градусах (°):

h = L ⋅ tg(α) , где α – уклон в градусах

Для примера найдём превышение h, если расстояние L= 5м, а угол уклона α=45°:

h = 5 ⋅ tg(45) = 5 ⋅ 1 = 5 м

Как посчитать расстояние

Для того чтобы посчитать расстояние (L) необходимо знать превышение (h) и уклон (в процентах, в промилле или в градусах).

Если уклон в процентах (%):

L = h / _{Уклон в %} ⋅ 100

Если уклон в промилле (‰):

L = h / _{Уклон в ‰} ⋅ 1000

Если уклон в градусах (°):

L = h / tg(α) , где α – уклон в градусах

Для примера посчитаем расстояние (L), которое потребуется железной дороге, чтобы подняться на (h =) 6 м при угле подъёма 30‰:

Климат местности

Угол наклона кровли также зависит от климатических условий, в которых сооружено здание. Почему? В местности, где крыши дома в большинстве случаев имеют минимальный угол наклона, часто дуют сильные ветра. Таким образом, конструкция уменьшает неблагоприятное воздействие ветра на крышу в целом. Кровли, которые имеют меньше 10 градусов уклона, практически не подвержены такому влиянию. Но здесь возникает вероятность срыва ветряным потоком кровельного материала.

Как посчитать оптимальный вариант? Специалисты рекомендуют возводить кровли в 35 градусов в местностях с небольшими ветряными нагрузками. При сильном ветре крыша должна быть 15-25 градусов.

Какой должен быть угол для мансард? Для его расчета необходимо длину торца разделить вдвое. А высота ската в торце стандартна (1,8 м).

В местностях, где часто выпадают большие осадки, угол наклона может быть равен 60 градусам.

Египетский треугольник

Также не стоит забывать и о такой геометрической фигуре, как египетский треугольник – прямоугольник с длинами сторон 3, 4, 5, причем совершенно не важно в каких величинах, ведь между катетами длиной 3 и 4 угол, равный ровно 90 градусов. Давайте проверим?. a 2 + b 2 = (3 2 + 4 2 ) = (9 + 16) = 25; √25 = 5

a 2 + b 2 = (3 2 + 4 2 ) = (9 + 16) = 25; √25 = 5.

Как проверить угол с помощью египетского треугольника?

Отмерьте на одной стене отрезок длиной 3 метра, а на другой – отрезок длиной 4 метра. Теперь измеряем расстояние между двумя этими отметками точно так же, как в способе с теоремой Пифагора. Если получившийся результат кратен 5, то в том, что полученный угол равен 90 градусов, можно не сомневаться.

Градусы электрические: отклонение между напряжением и током

Ну, синус? Ну, косинус? И что тут такого? Спросим любого человека, например, возле пивного ларька, что такое синус и как давно он пользовался косинусом после школы. Что услышим в ответ?! Во, именно «это» и услышим.

Вместе с тем мы постоянно живем, можно сказать, под градусом, точнее, под косинусом! Ежедневно мы пользуемся электричеством: нажимаем кнопки и выключатели, и дело с концом – все светится, крутится, работает.

Чтобы электричество выполняло свое предназначение, нужно электрическое напряжение и электрический ток. Обе «субстанции» должны быть вместе и одновременно. Но эти две величины могут иметь между собой угол отклонения, измеряемый «косинусом фи», как выражаются энергетики на своем профессиональном языке.

Если отклонение напряжения от тока есть ноль градусов, то электрическая мощность будет получена умножением величины напряжения на величину тока.

Допустим, подключаем электрообогреватель. Он начинает излучать тепло, равное по мощности этой самой величине: напряжение 220В (двести двадцать вольт) умножить на ток, скажем, 5А (пять ампер) равно 1КВт (1 киловатт) мощности. Становится тепло!

Если между напряжением и током есть отклонение, хотя бы на 1 градус, то придется перемножать не только напряжение и ток, но и полученный результат дополнительно умножать на косинус угла отклонения. Ноль градусов отклонения – косинус равен единице, умножение на единицу ничего не меняет. А вот косинус всего лишь 1-го градуса возможного отклонения уже меньше единицы. Не намного, но меньше. Это значит, что греть наша батарея будет уже слабее.

Чем больше отклонение электрического напряжения от электрического тока, чем будет больше между ними градусов так называемого угла «фи». Тем слабее будут греть батареи, хуже станет накал лампочек, и вообще будет меньше электричества.

И не говорите теперь, что косинус – это абстракция, которую мы оставили в школе навсегда…

Виды углов

Есть разные типы углов и у каждого своё название:

• острый
• прямой
• тупой
• развернутый
• выпуклый
• полный

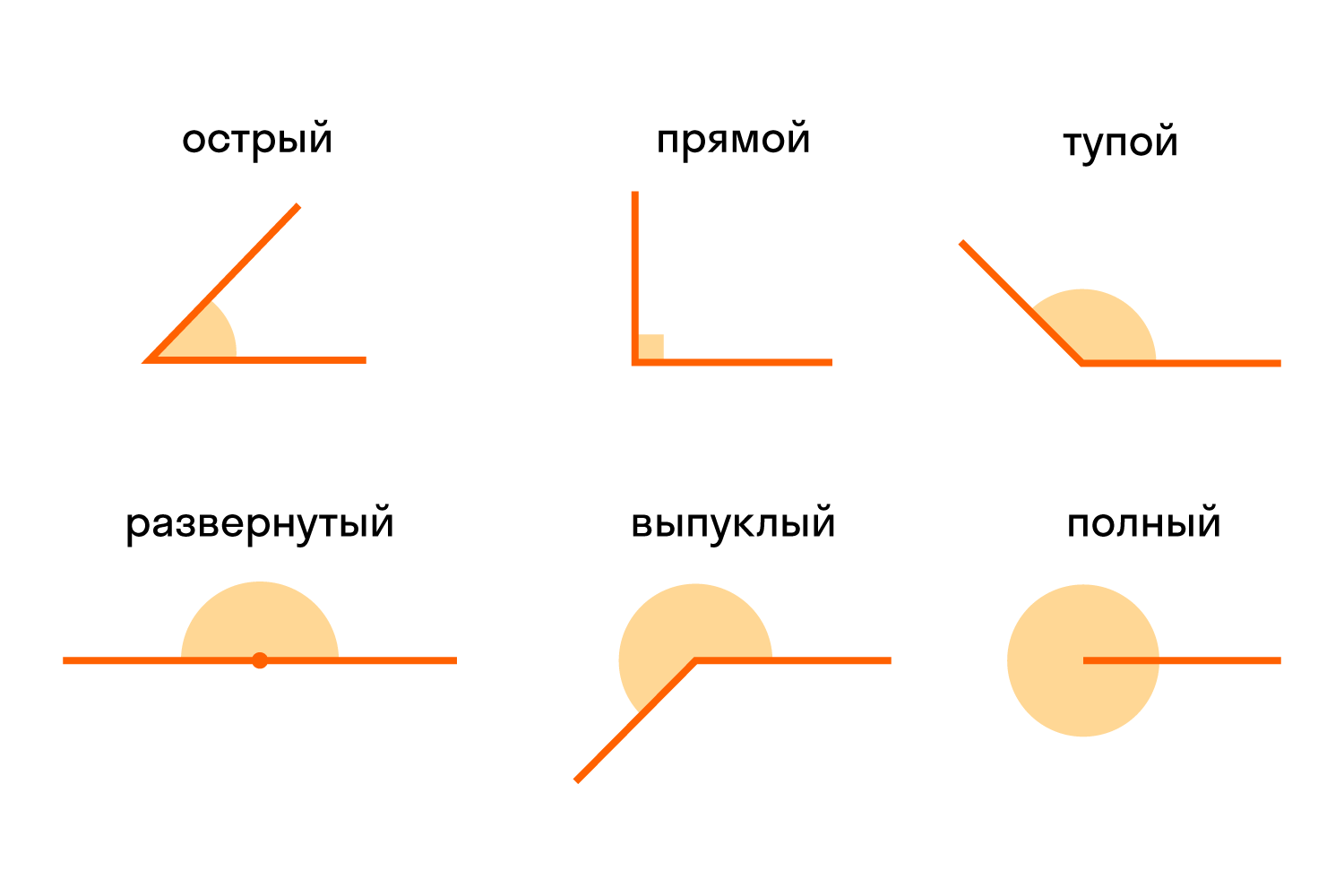
Различать виды углов в геометрии важно. Определять можно на глаз или с помощью линейки

Острый угол — это угол, который меньше прямого угла, то есть < 90°.

Прямой угол — это угол, стороны которого перпендикулярны друг другу. Прямой угол всегда равен половине развернутого угла, то есть = 90°.

Если два смежных угла равны между собой, то каждый из них является прямым. Для удобства прямой угол обозначается уголком. Вот так:

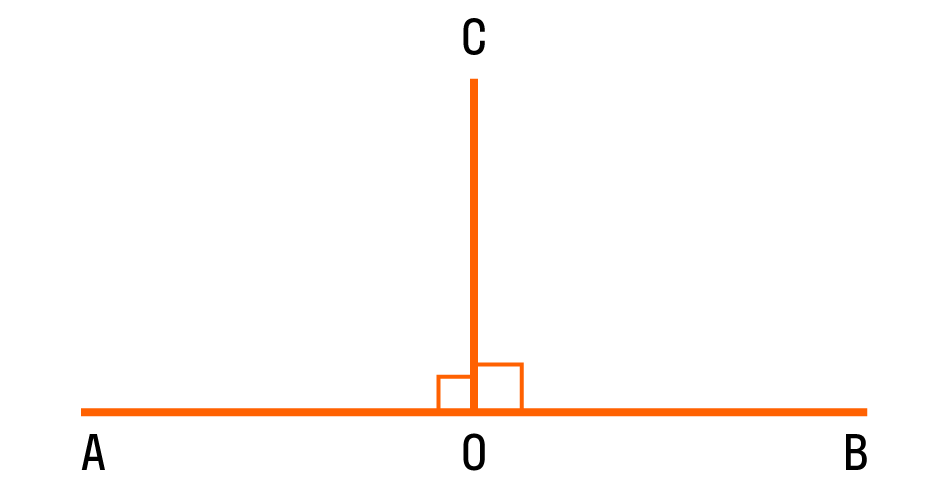
На картинке изображены два прямых угла ∠AOC и ∠COB. Общая сторона OC перпендикулярна прямой AB, а точка O — основание перпендикуляра.

Развернутый угол — это открытый угол, который образован двумя лучами и равен сумме двух прямых углов. Развернутый угол равен 180°. Как выглядит развернутый угол показано на первой картинке.

Неразвернутый угол — это любой угол, который не является развернутым, то есть не равен 180°.

Тупой угол — это угол, который больше прямого угла, но меньше развернутого:
90° < тупой угол < 180°.

Выпуклый угол — это угол, который больше развернутого угла, но меньше полного:
180° < выпуклый угол < 360°.

Полный угол — это угол, обе стороны которого совпадают с одним лучом. Он равен сумме четырех прямых углов, то есть = 360°.

Прилежащие углы — это пара углов с общей вершиной и стороной, другие стороны при этом лежат по разные стороны от общей стороны.

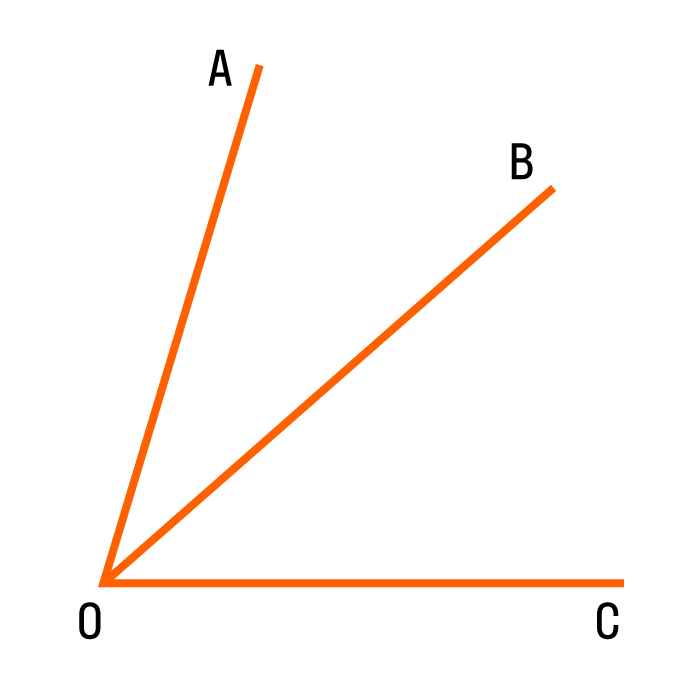
На картинке мы видим два прилежащих угла ∠AOB и ∠BOC, общую вершину O и общую сторону OB.

Можно сформулировать определение по-другому: если из вершины любого угла провести луч, разделяющий угол на два, то образованные углы будут прилежащими.

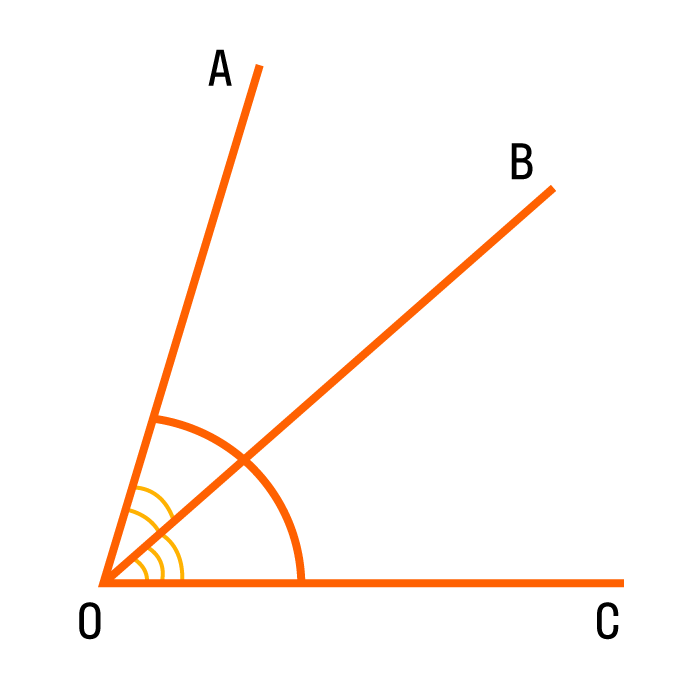
Чтобы найти угол, который разделен лучом, нужно сложить полученные углы: ∠AOB = ∠AOC + ∠COB. Из этого можно выделить следующие верные разности:

• ∠AOC = ∠AOB — ∠COB,
• ∠COB = ∠AOB — ∠AOC.

Как высчитать угол прямоугольного треугольника в градусах?

Если известны размеры трёх сторон, как высчитать угол в градусах?

Да, треугольник на рисунке не так, чтобы уж очень прямоугольный. Поэтому угол, который можно бы было посчитать за прямой (обозначен на рисунке знаком вопроса), приходится считать по теореме косинусов

1010^2 = 600^2 + 800^2 – 2 cos(a) 600 * 800

cos a = -(1010^2 – 600^2 – 800^2 )/ (2*600*800)=-0,20937

По табличке Брадиса или в своём супер-пупер телефоне находим: 91,2 градуса

Для вычисления углов необходимо обратиться к тригонометрии.

Нам необходимо вычислить величину острого угла А. Для этого используем формулу синуса: ВС/АС (800:1010) = 0,79207920792079.

Зная синус угла А, смотрим в таблицу Брадиса и определяем, что наш угол А равен примерно 52 градусам.

Так как сумма углов треугольника равна 180 градуса, и нам известна величина углов В и А, то мы легко можем узнать величину угла С= 180 – 90-52=38.

Ответ: угол А 52 градуса, угол С 38 градусов.

Формула для определения конусности

Провести самостоятельно расчет конусности можно при применении различных формул. Стоит учитывать, что в большинстве случаев показатель указывается в градусах, но может и в процентах – все зависит от конкретного случая. Алгоритм проведения расчетов выглядит следующим образом:

1. K=D-d/l=2tgf=2i. Данная формула характеризуется тем, что конусность характеризуется двойным уклоном. Она основана на получении значения большого и меньшего диаметра, а также расстояния между ними. Кроме этого определяется угол.
2. Tgf=D/2L. В данном случае требуется протяженность отрезка, который связывает большой и малый диаметр, а также показатель большого диаметра.
3. F=arctgf. Эта формула применяется для перевода показателя в градусы. Сегодня в большинстве случаев применяются именно градусы, так как их проще выдерживать при непосредственном проведении построений. Что касается процентов, то они зачастую указываются для возможности расчета одного из диаметров. К примеру, если соотношение составляет 20% и дан меньший диаметр, то можно быстро провести расчет большого.

Как ранее было отмечено, конусность 1:5 и другие показатели стандартизированы. Для этого применяется ГОСТ 8593-81.

На чертеже вычисления не отображаются. Как правило, для этого создается дополнительная пояснительная записка. Вычислить основные параметры довольно просто, в некоторых случаях проводится построение чертежа, после чего измеряется значение угла и другие показатели.

Пример расчёта

А теперь ознакомимся, как рассчитать угол наклона крыши на конкретном примере. Для начала необходимо узнать высоту конька по отношению к основанию. Этот параметр зависит от предназначения чердака. Если это помещение будет использоваться в качестве мансарды, то нам понадобится ещё одна величина – длина фронтона или основания.

Как измерить угол наклона, если высота от основания кровли до конька составляет 1,8 метра, а длина фронтона принимается кратной 6 метрам. Для начала необходимо разделить «подошву треугольника» на две части, а затем вычисляют синус угла по теореме Пифагора.

В нашем случае, это значение синуса угла, который находится из соотношения прилежащей стороны к противолежащей. Сначала делим треугольник на две равные части 6/2=3. Теперь вычисляем синус нужного угла 3/1,8= 1,6. Заглядываем в таблицу Брадиса и видим, что это значение соответствует углу в 59 градусов.

Заказать пандус-конструктор

Пандус стационарный с резиновым покрытием и поручнями из стали AISI 304

Размеры : ширина пандуса 900мм, разворотная площадка 2100Х1500мм, регулируемая высота Материал каркаса : сталь с порошковой покраской Покрытие пандуса : противоскользящий настил Опорные поручни : Нержавеющая сталь AISI 304 Цена пандус-конструктора от: 19540 руб. пог. м

Пандус стационарный с алюминиевым покрытием и поручнями из стали AISI 304

Размеры : ширина пандуса 900мм, разворотная площадка 2100Х1500мм, регулируемая высота0- Материал каркаса : сталь с порошковой покраской Покрытие пандуса : алюминиевый настил Опорные поручни : Нержавеющая сталь AISI 304 Цена пандус-конструктора от: 17790 руб. пог. м

Пандус стационарный сс резиновым покрытием и поручнями из стали

Размеры : ширина пандуса 900мм, разворотная площадка 2100Х1500мм, регулируемая высота Материал каркаса : сталь с порошковой покраской Покрытие пандуса : противоскользящий настил Опорные поручни : с порошковой покраской Цена пандус-конструктора от: 15670 руб. пог. м

Пандус стационарный с алюминиевым покрытием и поручнями из стали

Размеры : ширина пандуса 900мм, разворотная площадка 2100Х1500мм, регулируемая высота- Материал каркаса : сталь с порошковой покраской Покрытие пандуса : алюминиевый настил Опорные поручни : с порошковой покраской Цена пандус-конструктора от: 13062 руб. пог. м

Как узнать угол наклона крыши

Между уклоном кровельных скатов и снежной нагрузкой имеется прямая зависимость. Если угол наклона крыши меньше 25 градусов, то коэффициент снежной нагрузки равен 1, а при углах, варьирующихся в пределах от 25 до 60 градусов, то этот коэффициент увеличивается до 1,25. Крыша с большим углом наклона не будет подвергаться снежным нагрузкам вообще, поэтому они не учитываются при расчетах.

Чтобы определить угол наклона крыши, нужно воспользоваться таблицей Брадиса и простой методикой: высота кровельной конструкции делится на длину фронтона, разделенную на два, после чего остается найти таблице угол, который соответствует полученному результату.

Высота крыши в коньке определяется следующим образом:

• Первым делом нужно рассчитать ширину пролета;
• Полученная величина делится на 2;
• Чтобы сделать расчет высоты конька, результат предыдущего расчета умножается на коэффициент, соответствующий определенному углу наклона.

На примере реализация такой методики расчета выглядит так: при ширине здания, равной 8 метрам, и 25-градусном уклоне кровли, расчетный коэффициент составляет 0,47. В итоге подстановки значений получается выражение следующего вида: 4х0,47 = 1,88 м. Полученная величина – это высота крыши, соответствующая имеющимся исходным данным.

Как сделать прямой угол между стенами.

Древнегреческие геометры и, в частности Евклид, старались зря, их знания до советских строителей так и не дошли. В том смысле, что прямоугольных помещений в советских домах не бывает. А бывают в лучшем случае в виде параллелограмма, усеченной трапеции или ромба, а в худшем и наиболее распространенном в виде неправильного четырехугольника. Это довольно часто затрудняет качественную отделку помещений. Приходится искать прямой угол самому. Сделать это в общем-то несложно.

Разметку проще всего производить на полу. Для этого Вам понадобятся:

• Маркер, мел или карандаш
• Строительный уровень, суровая нитка или строительный шнур.
• Рулетка.

С помощью строительного уровня или отвеса (проще — с помощью уровня, точнее — с помощью отвеса) определите выпирающие участки стен. В этих местах перенесите вертикальные отметки на пол. Проведите через 2 отметки вдоль каждой стены прямые линии так, чтобы остальные отметки (если они у Вас есть) остались между линией и стеной.

Если стены перпендикулярные это расстояние должно равняться

1.414 м более точно 1.41421356 м, но такая точность вам не понадобится.

Если расстояние (гипотенуза треугольника) больше, то у Вас вместо прямого угла между стенами тупой. Для того, чтобы получить прямой угол, приложите начало рулетки к точке пересечения линий в углу и нарисуйте небольшую дугу радиусом 1 м. Затем приложите начало рулетки к отметке на линии вдоль стены принятой за основу и нарисуйте небольшую дугу радиусом 1.414 м. Проведите через точку пересечения дуг и точку пересечения линий в углу прямую линию. Эта новая линия и будет контуром стены. Если это для Вас слишком сложно, то просто отмерьте на гипотенузе 1.414 м от отметки у той стены которую вы приняли за основу. Проведите прямую линию через полученную отметку и точку пересечения линий в углу. В этом случае Вы получите не прямой угол, но все же намного ближе к прямому, чем тот который был.

Использование расчетного и оптимального уровня наполняемости

Также у пластиковой, асбестоцементной или чугунной канализационной трубы обязательно должен быть рассчитан уровень наполненности. Это понятие определяет, какой должна быть скорость движения потока в трубе, чтобы она не засорилась. Естественно, от наполненности также зависит уклон. Вычислить расчетную наполненность можно при помощи формулы:

• Н – уровень воды в трубе;
• D – ее диаметр.

Минимальный допустимый СНиП 2.04.01-85 уровень наполняемости, согласно СНиПа – Y=0,3, а максимальный Y=1, но в таком случае канализационная труба полная, а, следовательно, уклона нет, значит нужно выбирать 50-60%. На практике расчетная наполняемость лежит в диапазоне: 0,3 Гидравлический расчет на наполняемость и угол уклона

Ваша цель – рассчитать максимально допустимую скорость для устройства канализационного стока. Согласно СНиП, скорость движения жидкости должна быть не менее 0,7 м/с, что позволит отходам быстро проходить мимо стенок, при этом не прилипая.

Примем H=60 мм, а диаметр трубы D=110 мм, материал – пластмасса.

Следовательно, правильный расчет выглядит так:

60 / 110 = 0,55 = Y – это уровень рассчитанной наполненности;

Далее используем формулу:

K ≤ V√ y, где:

• К — оптимальный уровень наполненности (0,5 для пластмассовых и стеклянных труб или 0,6 для чугунных, асбестоцементных или керамических труб);
• V — скорость движения жидкости (минимально берем 0,7 м/с);
• √Y – квадратный корень расчетной заполняемости трубы.

0,5 ≤ 0,7√ 0,55 = 0,5 ≤ 0,52 – расчет верен.

Последняя формула является проверочной. Первая цифра – это коэффициент оптимальной наполненности, вторая после знака равенства – это скорость движения стоков, третья – это квадрат от уровня наполненности. Формула нам показала, что скорость мы выбрали правильно, то есть минимально возможную. В тоже время увеличить скорость мы не можем, так как нарушится неравенство.

Также угол можно выражать в градусах, но тогда Вам будет сложнее переходить на геометрические величины при установке наружной или внутренней трубы. Такое измерение предоставляет более высокую точность.

Уклон канализационных труб схематически

Таким же образом несложно определить уклон наружной подземной трубы. В большинстве случаев, коммуникации наружного типа имеют большие диаметры.

Следовательно на метр будет использоваться больший уклон. При этом есть еще определенный гидравлический уровень отклонения, который позволяет сделать уклон немного меньшим, чем оптимальный.

Резюмирую скажем, что согласно СНиП 2.04.01-85 пункт 18.2 (норма при установке систем отвода воды), при устройстве угла канализационных труб частного дома, нужно придерживаться таких правил:

1. На один погонный метр у трубы с диаметром до 50 мм, нужно выделять по 3 см уклона, но при этом у трубопроводов с диаметром 110 мм понадобится 2 см;
2. Максимально допустимое значение, как для внутренней, так и для наружной напорной канализации – это общий уклон трубопровода от основания до конца 15 см;
3. Нормы СНиП требуют обязательного учета уровня промерзания грунта для установки наружной канализационной системы;
4. Для определения правильности выбранных углов необходимо проконсультироваться со специалистами, а также проверить выбранные данные по формулам выше;
5. При монтаже канализации в ванной, можно сделать коэффициент наполненности, соответственно и уклон трубы, самым минимальным. Дело в том, что из этой комнаты вода выходит преимущественно без абразивных частиц;
6. Перед работой нужно обязательно составлять план.

Совет от эксперта:

Не стоит путать методику установки канализационных труб в квартире и доме. В первом случае часто используется вертикальный монтаж. Это когда от унитаза или душевой кабинки устанавливается вертикальная труба, а уже она переходит в магистральную, выполненную под определенным уклоном.

Такой способ может быть применен, если, к примеру, душевая или умывальник находится на чердаке дома. В свою очередь, укладка внешней системы начинается сразу же от колец унитаза, септика или умывальника.

Чтобы при установке выдержать нужный угол, рекомендуется заранее копать траншею под уклоном, а по неё натянуть бечевку. Тоже самое можно сделать и по полу.

Высота конька тоже зависит от угла ската

При расчетах любой кровли за ориентир всегда берется прямоугольный треугольник, где катеты – это высота ската в верхней точке, то есть в коньке или же переходе нижней части всей системы стропил в верхнюю (в случае с мансардными кровлями), а также проекция длины конкретного ската на горизонталь, которая представлена перекрытиями. Здесь есть только одна постоянная величина – это длина крыши между двумя стенами, то есть длина пролета. Высота коньковой части будет меняться в зависимости от угла наклона.

Высота конька может меняться в зависимости от угла наклона

Спроектировать кровлю помогут знания формул из тригонометрии: tgA = H/L, sinA = H/S, H = LхtgA, S = H/sinA, где А – это угол ската, Н – высота кровли к области конька, L – ½ всей длины пролета кровли (при двухскатной крыше) либо вся длина (в случае односкатной кровли), S – длина самого ската. Например, если известно точное значение высоты коньковой части, то определяется угол наклона по первой формуле. Найти угол можно будет по таблице тангенсов. Если же в основе расчетов лежит угол кровли, то найти параметр высоты конька можно по третьей формуле. Длину стропил, имея значение угла наклона и параметров катетов, можно посчитать по четвертой формуле.

Таблица тангенсов