Что такое развертка конуса и как ее построить? формулы и пример решения задачи

Дно для конуса

Как сделать качественный конус, мы разобрались. Но следует отметить, что каждый из вышеперечисленных методов изготовления нуждается в одной маленькой доработке, конечно если это предусматривает будущая поделка.

Возможно вашему конусу потребуется дно. Сейчас мы расскажем, как его сделать правильно.

Первый способ

Дно для конуса (Шаг 1)

• возьмите свою готовую фигуру, поставьте на лист и обведите карандашом нижнюю часть;
• убираем конус, он нам пока не нужен;
• к полученному кругу добавляем с внешней стороны один сантиметр и проводим с помощью циркуля еще одну линию;
• радиус дна должен быть больше нижней части конуса, это обязательное условие;
• вырезаем круг;
• используя лишний сантиметр готового круга разрезаем его на зубчики, они будут приклеиваться во внутреннюю часть фигуры;
• загибаем зубья и смазываем их клеем;
• аккуратно приклеиваем полученное дно к конусу.

Фигура полностью готова.

Второй вариант

Этот способ слегка отличается от предыдущего. Как сделать дно по этому способу:

• измеряем ширину нижней части фигуры;
• от полученного числа отнимаем три миллиметра;
• рисуем круг на другом листе с учетом полученных показателей;
• на изображении сделайте припуск и уже полученную заготовку вырезайте;
• сгибаем припуск, наносим клей и приклеиваем изделие к низу конуса.

Таким образом вы получите точный геометрический макет.

Развертка на примере усеченного конуса

Развертку конуса можно получить автоматически используя приложение Оборудование: Развертки, либо построить конус листовым телом и развернуть его. Рассмотрим оба способа.

Построение развертки усеченного конуса, выполненного листовым телом

1. Создадим эскиз на плоскости XY (кликнуть левой кнопкой мыши на плоскость XY и выбрать из всплывающего меню команду «Создать эскиз»);
2. Построим в эскизе окружность произвольного диаметра с центром в начале координат
3. Выйдем из эскиза кликнув по индикатору режима и создадим смещенную от XY плоскость. Расстояние выберем любое.Команда»Смещенная плоскость»размещена на инструментальной панели «Вспомогательные объекты» (размещение команды показано на рисунке). После вызова команды необходимо кликнуть по плоскости XY и задать расстояние на Панели параметров, после чего подтвердить создание плоскости командой «Создать объект»
4. Создаем на смещенной плоскости эскиз, в эскизе выполняем построение окружности произвольного диаметра с привязкой центра к началу координат (аналогично пунктам 1-2). Выходим из эскиза кликнув левой кнопкой мыши по индикатору режима. В итоге деталь должна иметь следующий вид:
5. Строим усеченный конус командой «Линейчатая обечайка», которая расположена на панели «Элементы листового тела» в наборе «Листовое моделирование».Запустив команду указываем Эскиз1 и Эскиз2, можно указать их в дереве, можно просто кликнуть по окружностям в окне модели. Также требуется задать толщину стенки усеченного конуса на Панели параметров. Для подтверждения создания тела нажимаем кнопку «Создать объект»
6. Усеченный конус построен, теперь необходимо выполнить его развертку. Для этого воспользуемся командой «Развернуть» с Панели быстрого доступа. После вызова команды кликнем по конической грани и нажмем «Создать объект» . Перейти от развертки к усеченному конусу можно отжав режим развертка
7. Остается перенести данную развертку с 3D в чертеж. Для этого создаем новый документ чертеж. Заходим по пути: Главное текстовое меню — Вставка — Вид с модели — Вид с модели…Указать деталь с разверткой (обязательно файл с деталью сохранить, иначе он не появится в списке). Поставить на Панели параметров галочку «Развертка». В результате будет построен вид с разверткой.

Построение развертки усеченного конуса с помощью приложения

Приложение Оборудование: Развертки позволяет построить развертку деталей имеющих форму:

• усеченного цилиндра;
• прямого кругового конуса;
• усеченного прямого кругового конуса;
• кругового конуса, усеченного не параллельно основанию;
• наклонного кругового конуса, усеченного параллельно основанию;
• тройников;
• перехода с прямоугольного сечения на круглое;
• труб прямоугольного и многоугольного сечения;
• отводов.

Строить развертки поверхностей, имеющих форму типа:

• цилиндра;
• конуса;
• тора;
• сферы.

Приложение Оборудование: Развертки входит в Машиностроительную конфигурацию КОМПАС и приобретается отдельно от базового КОМПАС. Если Машиностроительная конфигурация на Вашем компьютере установлена, требуется подключить Приложение. Для этого нужно зайти по пути: Главное текстовое меню — Приложения — Конфигуратор — раскрыть в списке раздел Оборудование — выделить строку Оборудование:Развертки и нажать на ссылку «Подключить»

После подключения Приложение появится в наборе инструментальных панелей. Нужно будет выбрать панель Оборудование: Развертки и на панели выбрать тип объекта, развертку которого мы хотим получить.

Построим развертку усеченного конуса, также как в первом примере. Выберем команду «Патрубок конический тип 1». На Панели параметров задаем данные по усеченному конусу: 2 диаметра и высоту и нажимаем «Создать объект»

Откроется окно записи файла в котором нужно указать имя документа

Получаем чертеж развертки с размерами:

Развертка на примере усеченного конуса

Развертку конуса можно получить автоматически используя приложение Оборудование: Развертки, либо построить конус листовым телом и развернуть его. Рассмотрим оба способа.

Построение развертки усеченного конуса, выполненного листовым телом

1. Создадим эскиз на плоскости XY (кликнуть левой кнопкой мыши на плоскость XY и выбрать из всплывающего меню команду «Создать эскиз»);
2. Построим в эскизе окружность произвольного диаметра с центром в начале координат
3. Выйдем из эскиза кликнув по индикатору режима и создадим смещенную от XY плоскость. Расстояние выберем любое.Команда»Смещенная плоскость»размещена на инструментальной панели «Вспомогательные объекты» (размещение команды показано на рисунке). После вызова команды необходимо кликнуть по плоскости XY и задать расстояние на Панели параметров, после чего подтвердить создание плоскости командой «Создать объект» 
4. Создаем на смещенной плоскости эскиз, в эскизе выполняем построение окружности произвольного диаметра с привязкой центра к началу координат (аналогично пунктам 1-2). Выходим из эскиза кликнув левой кнопкой мыши по индикатору режима. В итоге деталь должна иметь следующий вид:
5. Строим усеченный конус командой «Линейчатая обечайка», которая расположена на панели «Элементы листового тела» в наборе «Листовое моделирование».Запустив команду указываем Эскиз1 и Эскиз2, можно указать их в дереве, можно просто кликнуть по окружностям в окне модели. Также требуется задать толщину стенки усеченного конуса на Панели параметров. Для подтверждения создания тела нажимаем кнопку «Создать объект» 
6. Усеченный конус построен, теперь необходимо выполнить его развертку. Для этого воспользуемся командой «Развернуть» с Панели быстрого доступа. После вызова команды кликнем по конической грани и нажмем «Создать объект» . Перейти от развертки к усеченному конусу можно отжав режим развертка
7. Остается перенести данную развертку с 3D в чертеж. Для этого создаем новый документ чертеж. Заходим по пути: Главное текстовое меню — Вставка — Вид с модели — Вид с модели…Указать деталь с разверткой (обязательно файл с деталью сохранить, иначе он не появится в списке). Поставить на Панели параметров галочку «Развертка». В результате будет построен вид с разверткой.

Построение развертки усеченного конуса с помощью приложения

Приложение Оборудование: Развертки позволяет построить развертку деталей имеющих форму:

• усеченного цилиндра;
• прямого кругового конуса;
• усеченного прямого кругового конуса;
• кругового конуса, усеченного не параллельно основанию;
• наклонного кругового конуса, усеченного параллельно основанию;
• тройников;
• перехода с прямоугольного сечения на круглое;
• труб прямоугольного и многоугольного сечения;
• отводов.

Строить развертки поверхностей, имеющих форму типа:

• цилиндра;
• конуса;
• тора;
• сферы.

Приложение Оборудование: Развертки входит в Машиностроительную конфигурацию КОМПАС и приобретается отдельно от базового КОМПАС. Если Машиностроительная конфигурация на Вашем компьютере установлена, требуется подключить Приложение. Для этого нужно зайти по пути: Главное текстовое меню — Приложения — Конфигуратор — раскрыть в списке раздел Оборудование — выделить строку Оборудование:Развертки и нажать на ссылку «Подключить»

После подключения Приложение появится в наборе инструментальных панелей. Нужно будет выбрать панель Оборудование: Развертки и на панели выбрать тип объекта, развертку которого мы хотим получить.

Построим развертку усеченного конуса, также как в первом примере. Выберем команду «Патрубок конический тип 1». На Панели параметров задаем данные по усеченному конусу: 2 диаметра и высоту и нажимаем «Создать объект»

Откроется окно записи файла в котором нужно указать имя документа

Получаем чертеж развертки с размерами:

Уклоны и конусность — Техническое черчение

• Уклоном прямой ВС относительно прямой AB (фиг. 57, а) называется отношение:
• i=AC/AB=tga
• Конусностью называется отношение разности диаметров двух попе­речных сечений конуса к расстоянию между ними (фиг. 57,б)
• k=(D-d)/l=2tga
• Таким образом,
• k = 2i
• Уклон и конусность могут быть указаны: а) в градусах; б) дробью простой, в виде отношения двух чисел или десятичной; в) в процентах.
• Например: конусность, выраженная в градусах — 11°25’16″; отношением —  1:5; дробью —0,2; в процентах — 20%, и соответственно этому уклон в градусах — 5°42’38″; отношением — 1:10; дробью—0,1; в процентах —  10%.
• Для конусов, применяемых в машиностроении, OCT/BKC 7652 устанавливает следующий ряд нормальных конусностей — 1 :3; 1 :5; 1 :8; 1 : 10; 1 :15; 1:20; 1 :30; 1:50; 1 :100; 1:200, а также 30, 45, 60, 75, 90 и 120°.
• Допускаются в особых случаях также конусности 1:1,5; 1:7; 1:12 и 110°.

Если требуется через точку Л, лежащую на прямой AB (фиг. 57, в), провести прямую с уклоном i=l:n относительно AB, надо отложить от точки А по направлению данной прямой n произвольных единиц; в конце полученного отрезка AB восстановить перпендикуляр ЕС длиной в одну такую же единицу. Гипотенуза AС построенного прямоугольного треугольника определяет искомую прямую.

1. Для проведения прямой заданного уклона l:n через точку M, не лежащую на данной прямой AB, можно поступать двояко (фиг. 58):
2. 1)    построить в стороне прямоугольный треугольник KLN (или KLN1) с отношением катетов l:n, причём катет KL ll AB; затем через точку M провести искомую прямую MD (или MD1) параллельно гипотенузе вспомогательного треугольника KN (или LN1);

2)    опустить из точки M перпендикуляр ME на прямую AВ и при­нять его за единицу. По направлению прямой AB влево или вправо от точки E отложить n таких же отрезков; гипотенузы DM или MD1 по­строенных таким образом прямоугольных треугольников являются иско­мыми прямыми.

Построение конусности l:n относительно данной оси сводится к построению уклонов l:n/2 с каждой стороны оси.

Уклон или конусность чаще всего указывается в процентах или отношением единицы к целому числу. Рассмотрим эти способы построе­ния на примерах.

Пример 1. Требуется построить профиль сечения швеллера № 5 ОСТ 10017-39 (фиг. 59, а), если известно, что уклон его полок равен 10%

Размеры для построения берём из ОСТ 10017-39.

Проводим вертикальную прямую ek, равную h = 50 мм. Из точек e и k проводим прямые ec и kf, равные ширине полки b = 37 мм.

Ввиду того, что обе полки швеллера одинаковы, ограничимся построе­нием только одной из них. Откладываем на прямой ec от точки с отре­зок cm, равный (b-d)/2.

В точке m на перпендикуляре к прямой ec от­кладываем отрезок mn, равный t = 7 мм. Через точку n проводим прямую np параллельно ec, равную 50 мм.

• Перпендикулярно к np из точки p проводим отрезок ps, равный по длине десяти процентам отрезка np. Величина его определяется из от­ношения:
• ps/np=10/100,
• откуда
• ps=10*50/100=5 мм.

Прямая sn является искомой прямой, имеющей уклон 10% по отно­шению к ec. Дальнейшее построение профиля не представляет затруд­нений.

Отрезок np можно взять любой длины. Чем больше его величина, тем точнее будет построена прямая уклона. Однако для удобства вы­числения следует принимать отрезок np таким, чтобы длина его, выра­жаемая в миллиметрах, оканчивалась на 0 или 5.

П p и м e p 2. Построить профиль сечения двутавра № 10 ОСТ 10016-39 (фиг. 59, б), если известно, что уклон полок его равен 1:6. Размеры для построения берём из ОСТ 10016-39.

Проводим горизонтальную прямую cc, равную ширине полки b = = 68 мм. Через точку e, являющуюся серединой ширины полки, прово­дим вертикальную линию. Откладываем от точки с отрезок mс, равный

(b-d)/4. В точке m, перпендикулярно к отрезку cc, проводим прямую и

на ней откладываем отрезок mn, равный t=6,5 мм. Через точку n проводим горизонтальную прямую np, равную 30 мм, которая будет служить катетом прямоугольного треугольника. Чем длиннее катет, тем точнее будет построен уклон. Для удобства принимают длину отрезка np кратной шести, тогда второй катет будет равен целому числу. Вели­чина второго катета определяется из формулы

1. i=ps/np=1/6
2. где i — заданный уклон.
3. Подставив в формулу числовые значения, получим
4. ps=30/6=5 мм.

Откладываем в точке p под углом 90° к прямой np вычисленную длину второго катета, получим точку 5. Проводим через точки s и n прямую, которая и будет соответствовать искомой прямой, имеющей уклон 1 :6.

Построение сопряжений такое же, как и для швеллера в предыду­щем примере.

Дно для конуса

Как сделать качественный конус, мы разобрались. Но следует отметить, что каждый из вышеперечисленных методов изготовления нуждается в одной маленькой доработке, конечно если это предусматривает будущая поделка.

Возможно вашему конусу потребуется дно. Сейчас мы расскажем, как его сделать правильно.

Второй вариант

Этот способ слегка отличается от предыдущего. Как сделать дно по этому способу:

• измеряем ширину нижней части фигуры;
• от полученного числа отнимаем три миллиметра;
• рисуем круг на другом листе с учетом полученных показателей;
• на изображении сделайте припуск и уже полученную заготовку вырезайте;
• сгибаем припуск, наносим клей и приклеиваем изделие к низу конуса.

Таким образом вы получите точный геометрический макет.

Как построить развертку поверхности прямого усеченного конуса

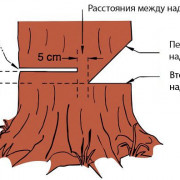
Делим основание конуса на 12 равных частей (вписываем правильную пирамиду). Данные элементы построения уже готовы из чертежа «Сечение конуса плоскостью частного положения».

Строим развертку боковой поверхности конуса, которая представляет собой круговой сектор. Центр его радиуса принимается за вершину конуса, а величина радиуса кругового сектора конуса равна длине образующей конуса, а длина дуги сектора равна длине окружности основания конуса. На дугу сектора переносим 12 хорд, которые определят ее длину, а также угол кругового сектора.

К центральной точке дуги сектора боковой развертки усеченного конуса пристраиваем основание конуса. Его основание проецируется в натуральную величину на горизонтальную плоскость проекции.

На развертке конуса к его основанию пристраиваем натуральную величину сечения.

Две крайние образующие конуса, которые формируют его основной контур, проецируются на фронтальную плоскость проекции в натуральную величину, поэтому их можно сразу переносить на развертку боковой поверхности конуса. Так как часть его срезана фронтально проецирующей плоскостью, то перенесем на развертку конуса только крайнюю правую усеченную образующую. Остальные усеченные образующие конуса проецируются на фронтальную плоскость проекций с искажением. Их натуральную величину находят способом вращения вокруг оси конуса до положения, параллельного фронтальной плоскости проекций.

Сам принцип нахождения натуральных величин образующих усеченного конуса сводится к тому, что проводят из точек пересечения образующих с плоскостью горизонтальную прямую до крайней правой (левой) образующей и на ней отмеряют натуральные их величины. Все действия проводят на фронтальной плоскости проекции.

На каждой образующей, лежащей на развертке боковой поверхности конуса, откладываем действительные длины усеченных образующих. Полученные точки соединяем плавной кривой линией команда Сплайн в Автокад.

Мы выполнили задачу начертательной геометрии на построение развертки усеченного конуса, но чтобы не возникло проблем во время ее защиты (когда я обучался, каждая курсовая по начертательной геометрии защищалась), еще раз рассмотрим принцип вращения для нахождения натуральной величины усеченной образующей конуса.

«Их натуральную величину находят способом вращения вокруг оси конуса до положения, параллельного фронтальной плоскости проекций.» Когда мы вращаем образующую прямого конуса до положения параллельного фронтальной плоскости проекции, то ее траектория описывает дугу на горизонтальной плоскости проекции, а на фронтальной прямую!

Вы можете не проводить линии связи с горизонтальной плоскости проекции на фронтальную, ведь очевидно, что точка будет лежать на крайней основной образующей контура конуса для каждой образующей при нахождении ее натуральной величины. Поэтому сам принцип вращения по нахождению натуральной величины образующих конуса сводится к проведению из точек усеченных образующих горизонтальной прямой до основной образующей контура конуса.

В видеоуроке очень наглядно и подробно показан принцип построения развертки прямого усеченного конуса.

Какой инструмент используется для забивания иглы абиссинского колодца?

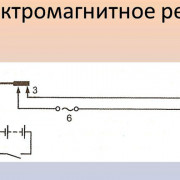
Кувалда

Самый простой и варварский способ забить иглу – кувалдой. Если у Вас есть опыт аккуратного обращения с этим могучим инструментом, возможно даже всё закончится хорошо и никакое резьбовое соединения у Вас под землей не треснет. Плюсы данного способа – кувалду легко найти, не нужно заморачиваться со специальным оборудованием для забивания. Минусы – при ударах кувалдой невозможно направить всю энергию удара вниз, строго по оси скважинной иглы. А значит, труба будет гнуться набок, плющится. Нагрузка на резьбовые соединения увеличивается. Если Вы приняли решение забивать иглу кувалдой, не бейте по куску трубы, который засаживаете в землю. Накрутите на трубу стальную муфту и используйте кусок трубы с резьбой, ввинтив ее в муфту. Такие наконечники трубы продаются в строительных магазинах под наименованием «резьба» и стоят копейки. Сплющили одну – заменили и продолжили забивать дальше.

Создаем новогоднюю елку

Из готового бумажного конуса можно создать отличное новогоднее украшение в виде елочки. Материалы при этом используются самые разнообразные, но общая система изготовления остается общей.

• На бумажный конус наклеивается скотч или пищевая пленка.
• Поверх них, с помощью ПВА или другого подходящего клея, прикрепляются толстые шерстяные нитки.
• После того, как они хорошо засохнут, нужно вынуть из них конус. Нити должны сохранить его форму.
• Останется только добавить элементы для украшения. Это могут быть небольшие вязаные шарики, звездочки из блестящей бумаги или любые другие материалы, оказавшиеся под рукой.

Для создания новогодней елочки можно воспользоваться совершенно другой техникой. На помощь придет папье-маше, с помощью которой можно тоже сделать бумажный конус. Конечно, материала и времени потребуется гораздо больше, но и готовая конструкция получится прочной и статной.

• Для работы потребуются газетные или журнальные обрезки. Подойдет практически любая бумага. Также необходима основа. Можно взять любой пластиковый конус, например – из детских игрушек. Он не пострадает при процессе изготовления.
• Выбранную основу обмазывают ПВА и накладывают на неё слой бумаги. Когда он подсохнет, можно наносить следующий. Таким образом процесс продолжается, пока не наберется достаточная толщина.
• Теперь нужно извлечь основу. Иногда для этого приходится разрезать фигуру.
• Затем вместо основы можно пометить внутрь стержень, который будет выполнять роль каркаса.

Остается лишь склеить разрезанные половинки обратно, и можно приступать к декорированию будущей елки. Например, её реально покрасить или обмотать нитками, как на фото ниже. Такая схема позволит создать любые варианты елочек, в зависимости от желания и имеющейся основы.

Круглый конус в геометрии

Приведем геометрическое определение этой фигуры. Круглым конусом называется поверхность, которая образована прямыми отрезками, соединяющими все точки некоторой окружности с одной-единственной точкой пространства. Эта единственная точка не должна принадлежать плоскости, в которой лежит окружность. Если вместо окружности взять круг, то указанный способ также приводит к получению конуса.

Вам будет интересно:Юридический колледж в Иваново: специальности, приемная комиссия, отзывы

Круг называется основанием фигуры, его окружность — это директриса. Отрезки, соединяющие точку с директрисой, называются генератрисами или образующими, а точка, где они пересекаются — это вершина конуса.

Круглый конус может быть прямым и наклонным. Обе фигуры показаны ниже на рисунке.

Разница между ними заключается в следующем: если перпендикуляр из вершины конуса падает точно в центр окружности, то конус будет прямым. Для него перпендикуляр, который называется высотой фигуры, является частью его оси. В случае конуса наклонного высота и ось образуют некоторый острый угол.

Ввиду простоты и симметричности фигуры далее будем рассматривать свойства только прямого конуса с круглым основанием.

Построение развертки конуса на бумаге

Для выполнения этой задачи понадобится лист бумаги, карандаш, транспортир, линейка и циркуль.

В первую очередь начертим прямоугольный треугольник со сторонами 3 см, 4 см и 5 см. Его вращение вокруг катета в 3 см даст искомый конус. У фигуры r = 3 см, h = 4 см, g = 5 см.

Построение развертки начнем с рисования циркулем окружности радиусом r. Ее длина будет равна 6*pi см. Теперь рядом с ней нарисуем еще одну окружность, но уже радиусом g. Ее длина будет соответствовать 10*pi см. Теперь нам нужно от большой окружности отрезать круговой сектор. Его угол φ равен:

Теперь откладываем транспортиром этот угол на окружности с радиусом g и проводим два радиуса, которые будут ограничивать круговой сектор.

Таким образом, мы построили развертку конуса с указанными параметрами радиуса, высоты и образующей.

Задача на определение диаметра через известную площадь конуса и его образующую

Дан конус, площадь поверхности которого составляет 150 см 2 . Генератриса равна 14 см. Чему равен диаметр конуса?

Для получения ответа на поставленный вопрос используем описанную в статье методику. Сначала выпишем соответствующее уравнение:

r 2 + 14*r — 150/3,14 = 0

При получении последнего равенства мы разделили левую и правую его части на число Пи. Рассчитываем дискриминант D. Имеем:

D = 14 2 — 4*1*(-150/3,14) = 387,0828

Полученный дискриминант приведен с точностью до 0,0001. Формула для корней уравнения r имеет следующий вид:

Очевидно, что один из корней будет отрицательным. Его не будем вычислять. Определим лишь искомый положительный радиус фигуры:

r = (-14+√387,0828)/2 = 2,837 см

Чтобы найти диаметр конуса, остается умножить это значение на два и записать ответ: d = 5,674 см.

В конце отметим, что, зная два любых параметра круглого конуса прямого, можно определить любую его характеристику, включая объем и площадь поверхности.

Изготовление конуса без циркуля

Бывает так, что циркуля нет или пользоваться им не хочется, а изготовить правильный конус нужно срочно. Megamaster.info расскажет вам, как сделать конус из бумаги без применения циркуля.

Для работы вам потребуется:

• бумага;
• ножницы;
• скотч.

Приступаем к работе:

1. Из бумаги нам нужно вырезать треугольник. Фигура должна иметь длинный низ, и идентичные короткие боковины. Получается так называемая развёртка конуса.
2. Складываем углы бумаги так, чтобы край заготовки располагался посередине. Второй угол также сворачиваем. Оборачиваем эту часть фигуры вокруг предыдущего угла. У вас уже должно получиться что-то похожее на конус.
3. У изделия ну;но выровнять края. Аккуратно и тщательно затягиваем углы. Делаем это так, чтобы фигура не распалась.
4. Если вы заметили, что у изделия торчат лишние участки бумаги, это значит, что изначально треугольник был сделан неправильно. Ситуацию можно исправить переделыванием поделки, отрезанием лишних участков с помощью ножниц или простым загибанием остатков внутрь изделия.
5. Осталось закрепить фигуру, чтобы она не потеряла свою форму. Возьмите скотч и проклейте заготовку изнутри.

Конус без использования циркуля готов.