Усеченный конус: формула объема, площади поверхностей и другое

Элементы конуса

Определение. Вершина конуса

– это точка (K), из которой исходят лучи.

Определение. Основание конуса

– это плоскость, образованная в результате пересечения плоской поверхности и всех лучей, исходящих из вершины конуса. У конуса могут быть такие основы, как круг, эллипс, гипербола и парабола.

Определение. Образующей конуса

(L) называется любой отрезок, который соединяет вершину конуса с границей основания конуса. Образующая есть отрезок луча, выходящего из вершины конуса.

Формула. Длина образующей

(L) прямого кругового конуса через радиус R и высоту H (через теорему Пифагора): L2 = R2 + H2

Определение. Направляющая

конуса – это кривая, которая описывает контур основания конуса.

Определение. Боковая поверхность

конуса – это совокупность всех образующих конуса. То есть, поверхность, которая образуется движением образующей по направляющей конуса.

Определение. Поверхность

конуса состоит из боковой поверхности и основания конуса.

Определение. Высота

конуса (H) – это отрезок, который выходит из вершины конуса и перпендикулярный к его основанию.

Определение. Ось

конуса (a) – это прямая, проходящая через вершину конуса и центр основания конуса.

Определение. Конусность (С)

конуса – это отношение диаметра основания конуса к его высоте. В случае усеченного конуса – это отношение разности диаметров поперечных сечений D и d усеченного конуса к расстоянию между ними:

C =	D	и C =	D – d
H	h

где C – конусность, D – диаметр основания, d – диаметр меньшего основания и h – расстояние между основаниями. Конусность характеризует остроту конуса, то есть, угол наклона образующей к основанию конуса. Чем больше конусность, тем острее угол наклона. угол конуса α будет:

α = 2arctg	R
H

где R – радиус основы, а H – высота конуса.

Определение. Осевое сечение

конуса – это сечение конуса плоскостью, проходящей через ось конуса. Такое сечение образует равнобедренный треугольник, у которого стороны образованы образующими, а основание треугольника – это диаметр основания конуса.

Определение. Касательная плоскость

к конусу – это плоскость, проходящая через образующую конуса и перпендикулярна к осевому сечению конуса.

Определение. Конус, что опирается на круг, эллипс, гиперболу или параболу называется соответственно круговым, эллиптическим, гиперболическим

илипараболическим конусом (последние два имеют бесконечный объем).

Определение. Прямой

конус – это конус у которого ось перпендикулярна основе. У такого конуса ось совпадает с высотой, а все образующие равны между собой.

Формула. Объём кругового конуса

V =	1	πHR2
3

где R – радиус основы, а H – высота конуса. Формула. Площадь боковой поверхности

(Sb) прямого конуса через радиус R и длину образующей L: Sb = πRL

Формула. Общая площадь поверхности

(Sp) прямого кругового конуса через радиус R и длину образующей L: Sp = πRL + πR2

Определение. Косой (наклонный)

конус – это конус у которого ось не перпендикулярна основе. У такого конуса ось не совпадает с высотой.

Формула. Объём любого конуса

V =	1	SH
3

где S – площадь основы, а H – высота конуса.

Определение. Усеченный

конус – это часть конуса, которая находится между основанием конуса и плоскостью сечения, параллельная основе.

Формула. Объём усеченного конуса

V =	1	(S2H – S1h)
3

где S1 и S2 – площади меньшей и большей основы соответственно, а H и h – расстояние от вершины конуса до центра нижней и верхней основы соответственно.

Изготовление конуса без циркуля

Бывает так, что циркуля нет или пользоваться им не хочется, а изготовить правильный конус нужно срочно. Megamaster.info расскажет вам, как сделать конус из бумаги без применения циркуля.

Для работы вам потребуется:

• бумага;
• ножницы;
• скотч.

Приступаем к работе:

1. Из бумаги нам нужно вырезать треугольник. Фигура должна иметь длинный низ, и идентичные короткие боковины. Получается так называемая развёртка конуса.
2. Складываем углы бумаги так, чтобы край заготовки располагался посередине. Второй угол также сворачиваем. Оборачиваем эту часть фигуры вокруг предыдущего угла. У вас уже должно получиться что-то похожее на конус.
3. У изделия ну;но выровнять края. Аккуратно и тщательно затягиваем углы. Делаем это так, чтобы фигура не распалась.
4. Если вы заметили, что у изделия торчат лишние участки бумаги, это значит, что изначально треугольник был сделан неправильно. Ситуацию можно исправить переделыванием поделки, отрезанием лишних участков с помощью ножниц или простым загибанием остатков внутрь изделия.
5. Осталось закрепить фигуру, чтобы она не потеряла свою форму. Возьмите скотч и проклейте заготовку изнутри.

Конус без использования циркуля готов.

Обозначение конусности на чертеже

При создании технической документации должны учитываться все установленные стандарты, так как в противном случае она не может быть использована в дальнейшем

Рассматривая обозначение конусности на чертежах следует уделить внимание следующим моментам:

1. Отображается диаметр большого основания. Рассматриваемая фигура образуется телом вращения, которому свойственен диаметральный показатель. В случае конуса их может быть несколько, а изменение показателя происходит плавно, не ступенчато. Как правило, у подобной фигуры есть больший диаметр, а также промежуточной в случае наличия ступени.
2. Наносится диаметр меньшего основания. Меньшее основание отвечает за образование требуемого угла.
3. Рассчитывается длина конуса. Расстояние между меньшим и большим основанием является показателем длины.
4. На основании построенного изображения определяется угол. Как правило, для этого проводятся соответствующие расчеты. В случае определения размера по нанесенному изображению при применении специального измерительного прибора существенно снижается точность. Второй метод применяется в случае создания чертежа для производства неответственных деталей.

Простейшее обозначение конусности предусматривает также отображения дополнительных размеров, к примеру, справочную. В некоторых случаях применяется знак конусности, который позволяет сразу понят о разности диаметров.

Выделяют достаточно большое количество различных стандартов, которые касаются обозначения конусности. К особенностям отнесем следующее:

1. Угол может указываться в градусах дробью или в процентах. Выбор проводится в зависимости от области применения чертежа. Примером можно назвать то, что в машиностроительной области указывается значение градуса.
2. В машиностроительной области в особую группу выделяют понятие нормальной конусности. Она варьирует в определенном диапазоне, может составлять 30, 45, 60, 75, 90, 120°. Подобные показатели свойственны большинству изделий, которые применяются при сборке различных механизмов. При этом выдержать подобные значения намного проще при применении токарного оборудования. Однако, при необходимости могут выдерживаться и неточные углы, все зависит от конкретного случая.
3. При начертании основных размеров применяется чертежный шрифт. Он характеризуется довольно большим количеством особенностей, которые должны учитываться. Для правильного отображения используется табличная информация.
4. Для начала указывается значок конусности от которого отводится стрелка и отображается величина. Особенности отображения во многом зависит от того, какой чертеж. В некоторых случаях наносится большое количество различных размеров, что существенно усложняет нанесение конусности. Именно поэтому предусмотрена возможность использования нескольких различных методов отображения подобной информации.

На чертеже рассматриваемый показатель обозначается в виде треугольника. При этом требуется цифровое значение, которое может рассчитываться при применении различных формул.

Объем пирамиды

Для начала рассмотрим треугольную пирамиду. Вершину пирамиды примем за начало координат точку О, а ось Ох проведем перпендикулярно основанию, причем ось будет направлена от вершины пирамиды к основанию.

Пусть ось Ох пересечет основание АВС в точке М. Тогда ОМ – это высота, чью длину мы обозначим как h.

Далее построим сечение А₁В₁С₁, параллельное АВС. Это сечение пересечется с ОМ в точке ОМ₁. Тогда ОМ₁ – это координата х, характеризующая расположение сечения А₁В₁С₁.

Осталось составить выражение для площади ∆А₁В₁С₁. Так как АВ||A₁B₁, то ∠АВО и ∠А₁В₁О одинаковы как соответственные углы. Тогда у ∆АВО и ∆А₁В₁О есть два равных угла (ведь ∠АОВ у них общий), а потому эти треугольники подобны по первому признаку подобия. Это означает, что

Надо как-то найти значение коэффициента k, который, очевидно, как-то зависит от переменной х. Рассмотрим теперь ∆ОМВ и ∆ОМ₁В₁. Они прямоугольные, ведь ОМ перпендикулярен плоскостям этих треугольников. Также у них есть общий угол ∠ОВМ. Значит, они подобны, и поэтому

Итак, если пирамида имеет высоту h и площадь основания S, то объем пирамиды равен:

Выведенная нами формула справедлива для треугольной пирамиды. Однако если в основании пирамиды лежит произвольный многоугольник, то, разбив этот многоугольник на треугольники, мы разобьем и пирамиду на несколько треугольных пирамид. У них будет общая высота h и площади оснований S₁, S₂, S₃…, которые в сумме составляют площадь многоугольника S.

Объем треугольных пирамид рассчитывается по выведенной нами формуле:

Задание. В основании пирамиды высотой 15 лежит квадрат со стороной 4. Вычислите ее объем.

Решение. Сначала находим площадь основания. Для этого надо сторону квадрата умножить саму на себя:

Задание. В кубе АВСDA₁В₁С₁D₁ отмечены точки Е и F – середины ребер ВС и CD соответственно. Во сколько раз объем пирамиды С₁EFC меньше объема куба?

Решение. Обозначим длину ребра куба буквой а. Тогда его объем рассчитывается так:

Задание. Отрезок MN перпендикулярен плоскости пятиугольника АВСDE. Точка K, принадлежащая этой плоскости, делит отрезок MN в отношении 2:1. Во сколько раз объем пирамиды MABCDE больше объема пирамиды NABCDE?

Решение. Запишем формулы для объемов этих пирамид. При этом учтем, что MK – высота для MABCDE, а NK – это высота для NABCDE.

Далее рассмотрим такую фигуру, как усеченная пирамида. Ясно, что ее объем можно вычислить, если из объема исходной пирамиды вычесть объем отсеченной верхушки.

Снова рассмотрим пирамиду ОАВС, через которую проведено сечение А₁В₁С₁, параллельное основанию.

Обозначим площадь нижнего основания пирамиды как S₂, а площадь верхнего основания – как S₁. Далее высоту усеченной пирамиды (отрезок ММ₁) обозначим как h. Мы уже выяснили ранее, что основания АВС и А₁В₁С₁ – это подобные треугольники, причем коэффициент их подобия k равен отношению высот ОМ и ОМ₁. Тогда можно записать:

Далее используем основное свойство пропорции:

Далее числитель дроби мы раскладываем на множители, используя формулу разности кубов:

Задание. Основаниями усеченной пирамиды являются квадраты со сторонами 9 см и 5 см, а высота пирамиды составляет 6 см. Найдите ее объем.

Сначала вычислим площади оснований:

Наклонное сечение конуса

ЦЕЛЬ И ПОСТАНОВКА ЗАДАНИЯ. Чтобы научиться строить наклонное сечение конуса, внимательно изучите последовательность построения, а затем сделайте рисунок сечения конуса наклонными плоскостями.

РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ ЗАДАНИЯ

Сечение конуса наклонной плоскостью, параллельной одной образующей его боковой поверхности, – парабола, если же секущая плоскость рассекает все образующие, в сечении получается эллипс. Рассмотрите ортогональную проекцию такого сечения на рис. 5.173

Обратите внимание, что центр эллипса сечения не лежит на оси вращения конуса (в отличие от цилиндра) – это хорошо видно на ортогональной проекции (рис. 5.174)

С этим связаны некоторые различия в построении наклонного сечения конуса и цилиндра. Однако эти построения во многом схожи, поэтому сечение конуса представлено менее подробно и в меньшем количестве рисунков-стадий.

Начните рисунок наклонного сечения конуса с построения вспомогательных вертикальных сечений, проходящих через вертикальную ось конуса. Вспомогательное сечение 7 перпендикулярно наклонной секущей плоскости (рис. 5.175). Линия пересечения этого вспомогательного сечения с наклонной плоскостью – прямая а – фиксирует продольные габариты эллипса (точки А и В). Середина отрезка АВ – точка О – центр эллипса сечения. Вспомогательное сечение 2 перпендикулярно сечению 7 (рис. 5.176). Линия пересечения наклонной секущей плоскости со вспомогательной плоскостью

2 – прямая b – фиксирует точки С и D, через которые проходит эллипс сечения. Однако точки С и D не задают поперечных габаритов эллипса сечения. Чтобы найти эти габариты необходимо еще одно – третье вспомогательное сечение. Вспомогательное сечение 3 перпендикулярно первому и второму сечению и проходит параллельно основанию конуса через точку О (рис. 5.177). Линия пересечения наклонной секущей плоскости со вспомогательной плоскостью – прямая с – фиксирует поперечные габариты эллипса сечения – точки Е и F. Для более точного построения эллипса проведите через точки А. В, Е и F дополнительные линии, как бы описывая вокруг будущего эллипса прямоугольник. Теперь впишите в этот прямоугольник эллипс, который должен касаться сторон прямоугольника в точках А, В, Е и F, проходить через точки С и D, а также касаться образующих конуса (рис. 5.178).

Как правило, в рисунке каждый выбирает сам, какое количество точек для построения эллипса сечения является достаточным. Для начинающего может быть необходимо построить все перечисленные точки, опытному рисовальщику достаточно двух точек, определяющих продольные габариты. Для закрепления пройденного материала постройте еще одно наклонное сечение конуса (рис. 5.179).

Как и в сечении цилиндра, эллипс наклонного сечения конуса будет изображаться на перспективном рисунке как эллипс. Однако следует заметить, что на вашем рисунке его оси (как и в цилиндре) не совпадают с осями, определяемыми габаритными точками. Это хорошо видно на примере сечения конуса, изображенного на рис. 5.180. Оси, относительно которых эллипс симметричен на перспективном рисунке, выделены толстой линией.

Усеченный геометрический объект

Усеченная фигура представляет собой объект в пространстве, который состоит из двух оснований разной площади и конической боковой поверхности. В отличие от исходного конуса, его усеченный вариант не имеет вершины. Остальные линейные элементы для него такие же, как для конуса с вершиной. У усеченной фигуры также имеется две директрисы, ограничивающие каждое из оснований, и одна генератриса, которая опирается на линии направляющих кривых.

Рассматриваемый геометрический объект также бывает нескольких видов (эллиптический, наклонный). Чаще всего в задачах по геометрии встречается именно круглый прямой усеченный конус, который ограничен двумя круглыми основаниями.

Способы построения

Можно выделить два основных способа построения усеченного круглого геометрического объекта:

• из круглого прямого конуса;
• с помощью трапеции.

В первом случае необходимо взять коническую фигуру и режущую плоскость, которая будет параллельна основанию. После этого с помощью плоскости следует отсечь верхнюю часть конуса. Оставшаяся под плоскостью фигура будет усеченной

Следует отметить, что совершенно неважно, какая часть конуса с вершиной будет отсечена. Чем больше она будет, тем ближе окажутся друг к другу значения верхнего и нижнего радиусов в усеченной фигуре, то есть тем ближе она по форме будет походить на прямой цилиндр.

Если прямоугольную трапецию поставить на большее основание и вращать ее вокруг перпендикуляра h, то получится усеченный конус. В нем отрезки a и b будут радиусами оснований объемной фигуры, перпендикуляр h станет высотой, а наклонный отрезок g будет представлять собой длину образующей. Эти четыре линейных характеристики определяют рассматриваемую объемную фигуру. Следует заметить, что для однозначного построения фигуры достаточно лишь трех любых из них, например, высоты и двух радиусов.

Площадь поверхности

Поверхность усеченной фигуры, в отличие от полного конуса, образована тремя частями: два круглых основания и боковая поверхность. Площади круглых оснований вычисляются по известной формуле для круга: pi*r2. Для боковой поверхности следует выполнить следующие действия:

Разрезать ее вдоль образующей и развернуть на плоскости.
Обратить внимание, что полученная фигура представляет собой сектор круга, у которого в верхней его части вырезан другой маленький сектор.
Достроить мысленно усеченную фигуру до полного конуса и определить его высоту H и директрису G. Через соответствующие параметры усеченного конуса они будут выражаться следующим образом: G = r1*g/(r1-r2), H = h*r1/(r1-r2), здесь радиусы оснований r1 и r2 такие, что r1>r2.
Рассчитать площади большого и маленького круговых секторов, а затем вычесть из первой вторую

В итоге получится следующая простая формула: Sb = pi*g*(r1 + r2).

Площадь всей поверхности рассматриваемой фигуры вычисляется как сумма трех величин S1, S2 и Sb:

S = S1 + S2 + Sb = pi*r12 + pi*r22 + pi*g*(r1 + r2).

Для определения величины S необходимо знать три линейных параметра усеченного конуса: радиусы оснований и длину генератрисы.

Формула объема

Для определения объема следует воспользоваться приемами, подобными тем, которые описаны в методике определения площади поверхности. Для начала следует усеченный конус достроить до полного, затем вычислить объемы фигур с высотами H и H-h по уже известной формуле. Разница этих объемов даст искомую формулу для усеченной фигуры с круглыми основаниями:

V = 1/3*pi*r12*H — 1/3*pi*r22*(H-h).

Подставляя в это выражение равенство для высоты H через линейные характеристики усеченной фигуры, можно получить конечную формулу:

V = 1/3*pi*h*(r12 + r22 + r1*r2).

Это выражение можно переписать не через линейные параметры, а через площади оснований фигуры S1 и S2:

V = 1/3*h*(S1 + S2 + (S1*S2)^0,5).

Записанная формула объема может быть получена универсальным способом без привлечения известного выражения для полного конуса. Для этого необходимо использовать интегральное исчисление, разбивая при этом усеченный геометрический объект на бесконечное количество тонких круглых дисков. Их радиусы будут постепенно уменьшаться от r1 до r2. Этот метод вывода формулы для объема не отличается от аналогичного для полного круглого конуса, изменяются лишь пределы интегрирования.

Формула для определения конусности

Провести самостоятельно расчет конусности можно при применении различных формул. Стоит учитывать, что в большинстве случаев показатель указывается в градусах, но может и в процентах – все зависит от конкретного случая. Алгоритм проведения расчетов выглядит следующим образом:

1. K=D-d/l=2tgf=2i. Данная формула характеризуется тем, что конусность характеризуется двойным уклоном. Она основана на получении значения большого и меньшего диаметра, а также расстояния между ними. Кроме этого определяется угол.
2. Tgf=D/2L. В данном случае требуется протяженность отрезка, который связывает большой и малый диаметр, а также показатель большого диаметра.
3. F=arctgf. Эта формула применяется для перевода показателя в градусы. Сегодня в большинстве случаев применяются именно градусы, так как их проще выдерживать при непосредственном проведении построений. Что касается процентов, то они зачастую указываются для возможности расчета одного из диаметров. К примеру, если соотношение составляет 20% и дан меньший диаметр, то можно быстро провести расчет большого.

Как ранее было отмечено, конусность 1:5 и другие показатели стандартизированы. Для этого применяется ГОСТ 8593-81.

На чертеже вычисления не отображаются. Как правило, для этого создается дополнительная пояснительная записка. Вычислить основные параметры довольно просто, в некоторых случаях проводится построение чертежа, после чего измеряется значение угла и другие показатели.

Презентация на тему: » Конус Понятие конуса Понятие конуса Площадь поверхности конуса Площадь поверхности конуса Усечённый конус Усечённый конус.» — Транскрипт:

1

Конус Понятие конуса Понятие конуса Площадь поверхности конуса Площадь поверхности конуса Усечённый конус Усечённый конус

2

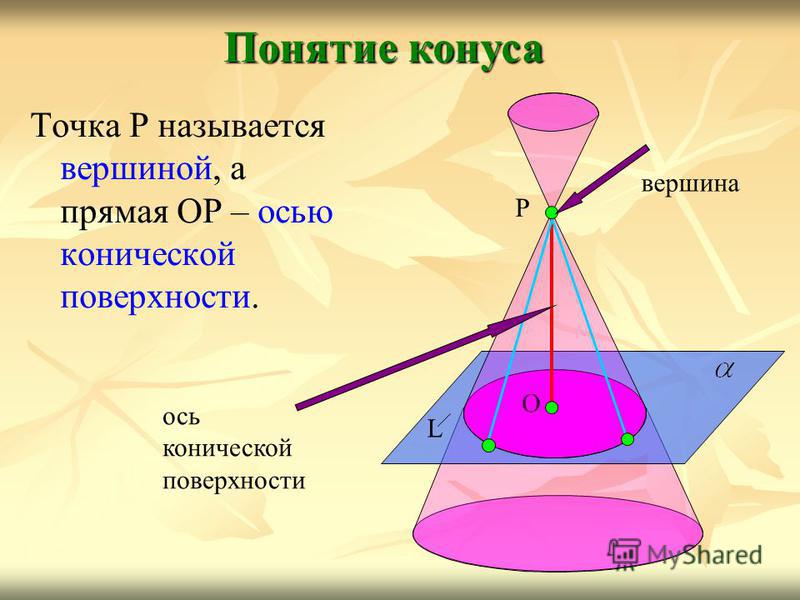
Понятие конуса Рассмотрим окружность L с центром О и прямую ОР, перпендикулярную к плоскости этой поверхности. Через точку Р и каждую точку окружности проведём прямую. Поверхность, образованная этими прямыми, называется конической поверхностью, а сами прямые – образующими конической поверхности. L О Р

3

Точка Р называется вершиной, а прямая ОР – осью конической поверхности. Понятие конуса L О Р вершина ось конической поверхности

4

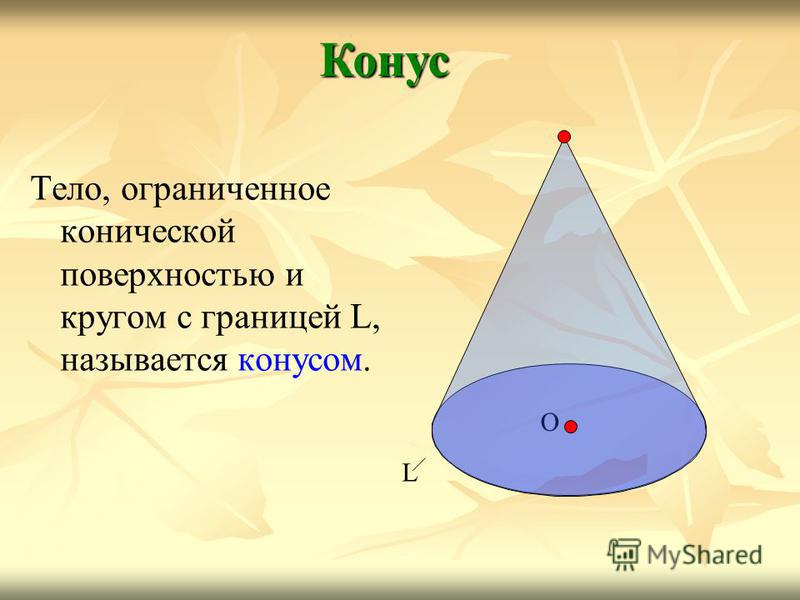
Тело, ограниченное конической поверхностью и кругом с границей L, называется конусом. Конус О L

5

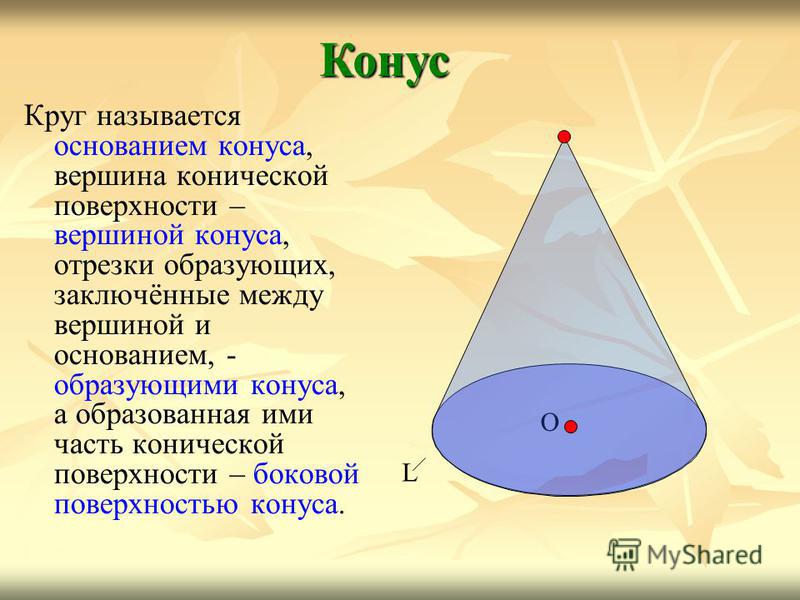
Круг называется основанием конуса, вершина конической поверхности – вершиной конуса, отрезки образующих, заключённые между вершиной и основанием, — образующими конуса, а образованная ими часть конической поверхности – боковой поверхностью конуса. Конус О L

6

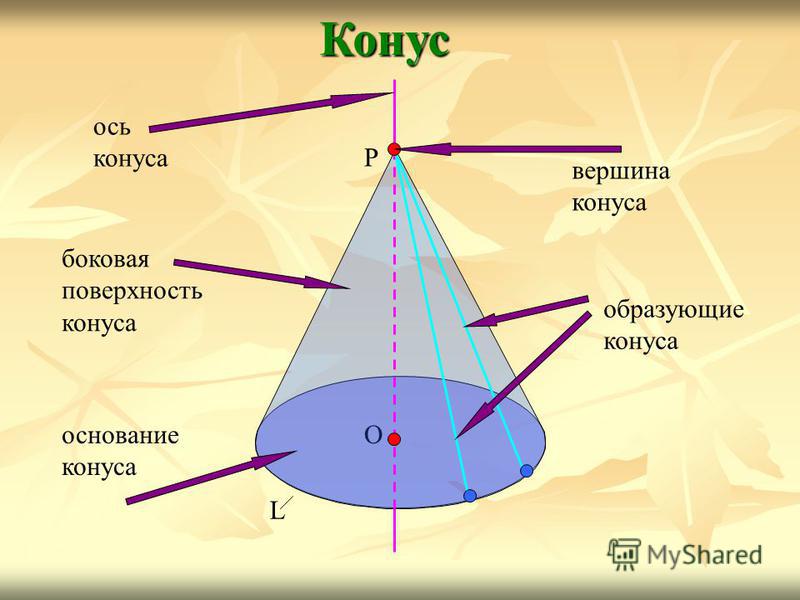
Конус О L Р ось конуса вершина конуса образующие конуса боковая поверхность конуса основание конуса

7

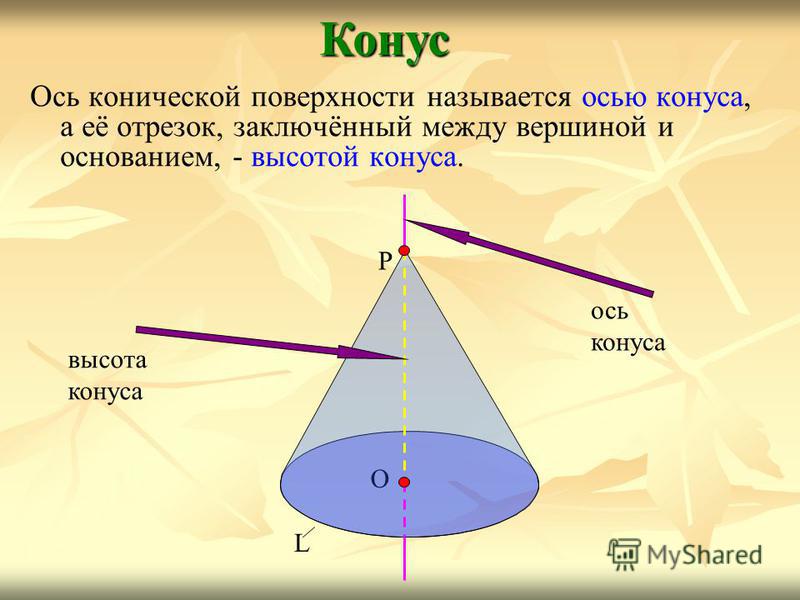
Ось конической поверхности называется осью конуса, а её отрезок, заключённый между вершиной и основанием, — высотой конуса.Конус О L Р ось конуса высота конуса

8

Конус может быть получен вращением прямоугольного треугольника вокруг одного из его катетов. Получение конуса

9

Если секущая плоскость проходит через ось конуса, то сечение представляет собой равнобедренный треугольник, основание которого – диаметр основания конуса, а боковые стороны – образующие конуса. Это сечение называется осевым. Сечение конуса О Р

10

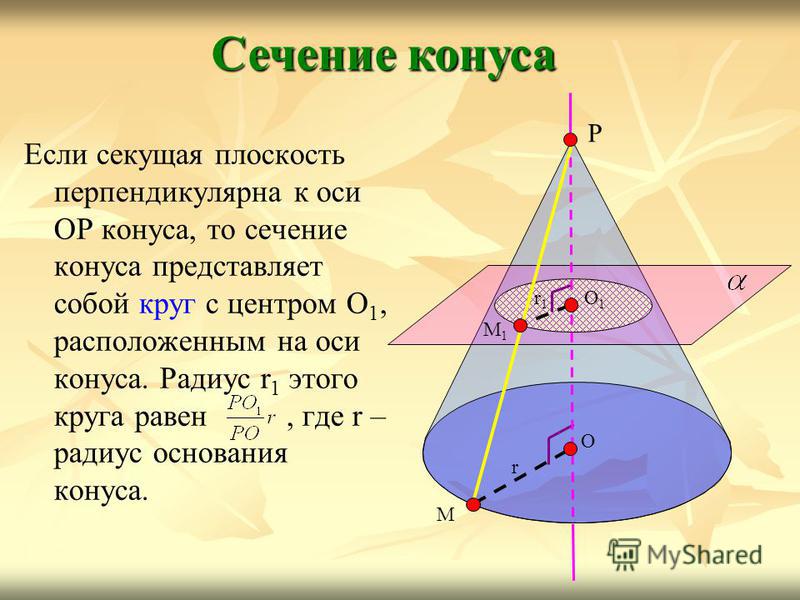
Если секущая плоскость перпендикулярна к оси ОР конуса, то сечение конуса представляет собой круг с центром О 1, расположенным на оси конуса. Радиус r 1 этого круга равен, где r – радиус основания конуса. Сечение конуса Р О М r О1О1 М1М1 r1r1

11

Проводя различные сечения одного и того же кругового конуса, причём любого, можно получить эллипс, параболу и гиперболу. При надлежащем наклоне секущей плоскости удаётся получить все типы конических сечений. Если считать, что конус не заканчивается в вершине, а простирается за неё, тогда у некоторых сечений образуются две ветви. Сечение конуса

12

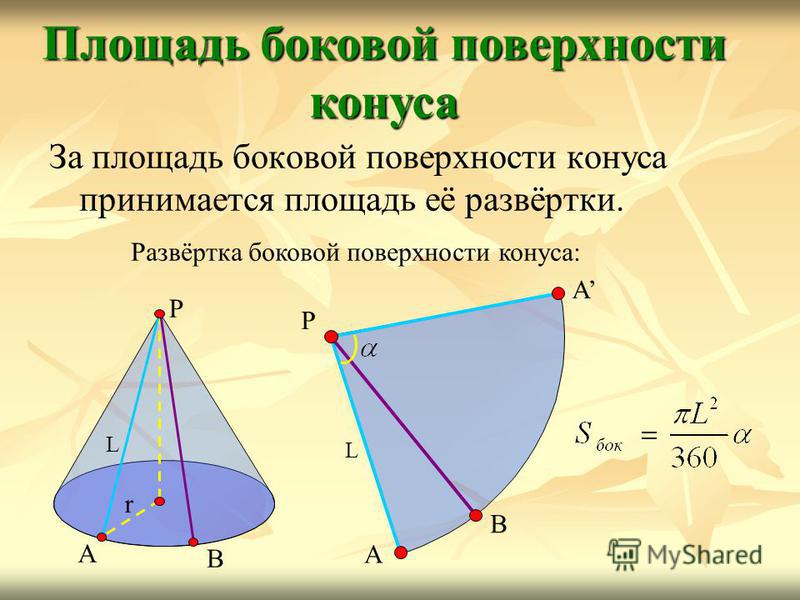
За площадь боковой поверхности конуса принимается площадь её развёртки. Площадь боковой поверхности конуса Развёртка боковой поверхности конуса: А В Р А L А В Р L r

13

Выразим через L и r. Так как длина дуги АВА равна, то, откуда Площадь боковой поверхности конуса А В Р А L Площадь боковой поверхности конуса равна произведению половины длины окружности основания на образующую.

14

Площадью полной поверхности конуса называется сумма площадей боковой поверхности и основания. Площадь полной поверхности конуса А В Р L r S кон = r 2 + rL S кон = r(r + L)

15

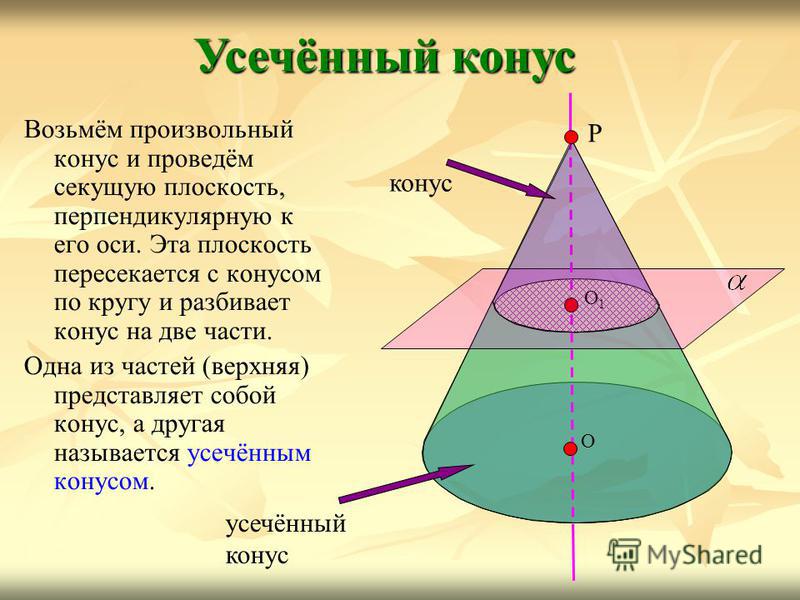
Возьмём произвольный конус и проведём секущую плоскость, перпендикулярную к его оси. Эта плоскость пересекается с конусом по кругу и разбивает конус на две части. Одна из частей (верхняя) представляет собой конус, а другая называется усечённым конусом. Усечённый конус Р О О1О1 конус усечённый конус

16

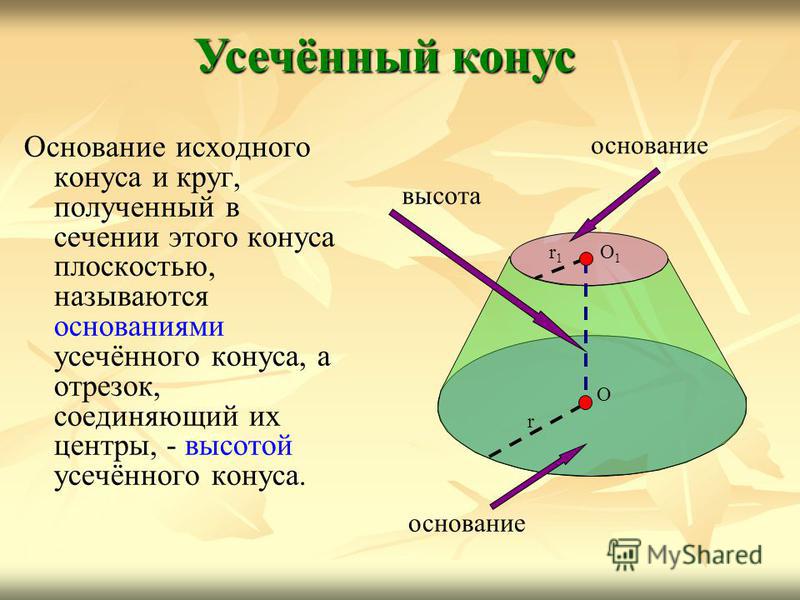
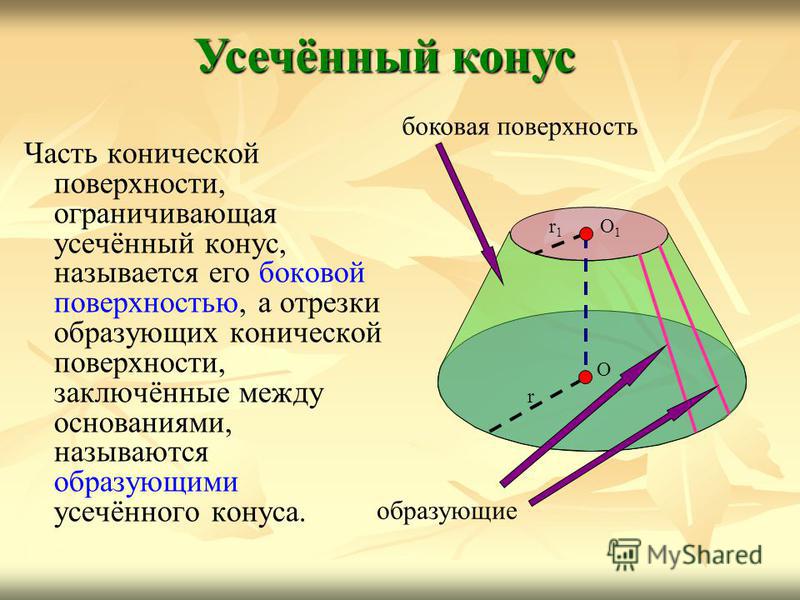
Основание исходного конуса и круг, полученный в сечении этого конуса плоскостью, называются основаниями усечённого конуса, а отрезок, соединяющий их центры, — высотой усечённого конуса. Усечённый конус О1О1 r1r1 r О основание высота

17

Часть конической поверхности, ограничивающая усечённый конус, называется его боковой поверхностью, а отрезки образующих конической поверхности, заключённые между основаниями, называются образующими усечённого конуса. Усечённый конус О1О1 r1r1 r О боковая поверхность образующие

18

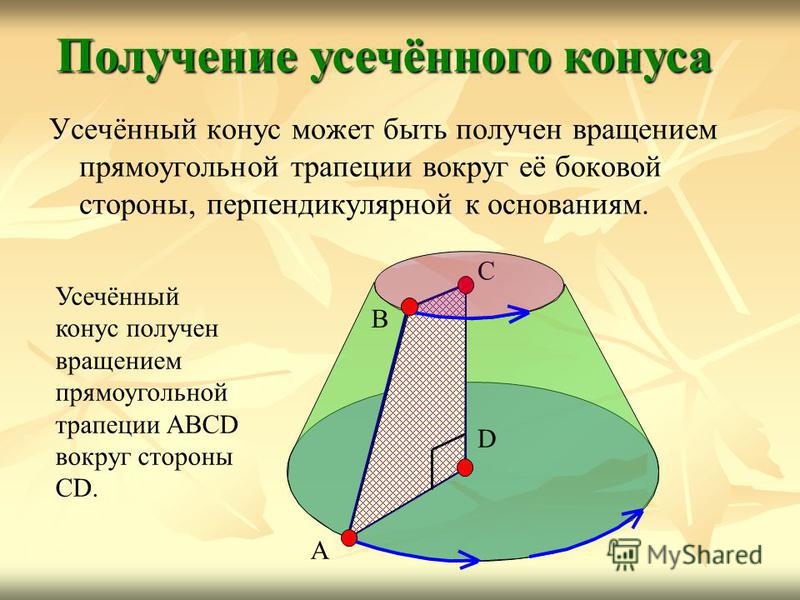
Усечённый конус может быть получен вращением прямоугольной трапеции вокруг её боковой стороны, перпендикулярной к основаниям. Получение усечённого конуса A B C D Усечённый конус получен вращением прямоугольной трапеции ABCD вокруг стороны CD.

19

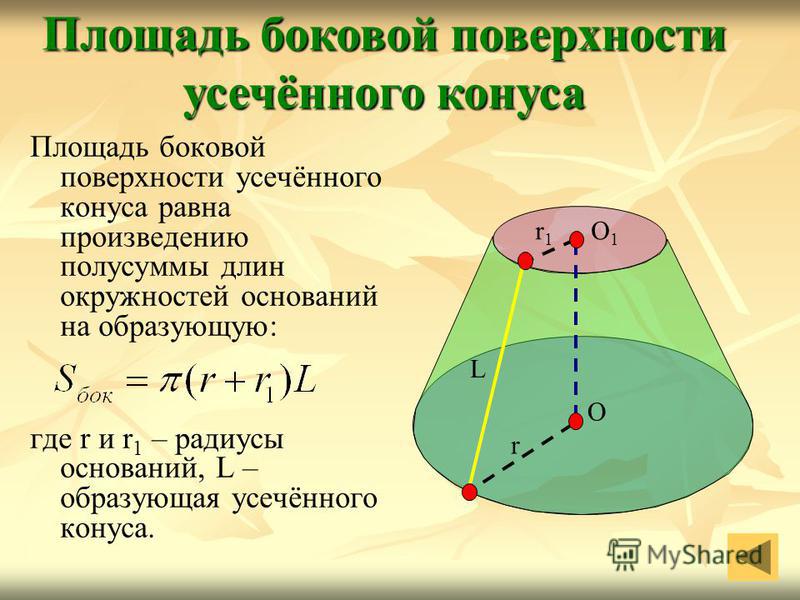
Площадь боковой поверхности усечённого конуса равна произведению полусуммы длин окружностей оснований на образующую: где r и r 1 – радиусы оснований, L – образующая усечённого конуса. Площадь боковой поверхности усечённого конуса О1О1 r1r1 r О L

Основные элементы конуса

• R – радиус круга, являющегося основанием конуса. Центр круга – точка D, диаметр – отрезок AB.
• h (CD) – высота конуса, одновременно являющаяся осью фигуры и катетом прямоугольных треугольников ACD или BCD.
• Точка C – вершина конуса.
• l (CA, CB, CL и CM) – образующие конуса; это отрезки, соединяющие вершину конуса с точками на окружности его основания.
• Осевое сечение конуса – это равнобедренный треугольник ABC, который образуется в результате пересечения конуса плоскостью проходящей через его ось.
• Поверхность конуса – состоит из его боковой поверхности и основания. Формулы для расчета площади поверхности, а также объема прямого кругового конуса представлены в отдельных публикациях.

Между образующей конуса, его высотой и радиусом основания есть взаимосвязь (согласно теореме Пифагора):

l2 = h2 + R2

Развёртка конуса – боковая поверхность конуса, развернутая в плоскость; является круговым сектором.

• длина дуги сектора равняется длине окружности основания конуса (т.е. 2πR);
• α – угол развёртки (или центральный угол);
• l – радиус сектора.

Примечание: Основные свойства конуса мы рассмотрели в отдельной публикации.